Question
Question: One quarter sector is cut from a uniform circular disc of radius \(R\). This sector has mass \(M\). ...
One quarter sector is cut from a uniform circular disc of radius R. This sector has mass M. It is made to rotate about a line perpendicular to its plane and passing through the center of the original disc. Its moment of inertia about the axis of rotation is
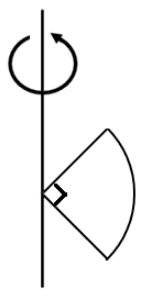
A. 21MR2
B. 41MR2
C. 81MR2
D. 2MR2
Solution
Disc must be in rotations so to calculate moment of inertia of disc we need disc with action with same axis and displacement. Calculate the moment of the whole disc about its axis and then determine the moment of inertia of the quarter cut.
Complete step by step answer:
If we consider the whole disc is initially rotating about its axis and since the mass of quarter of the cut is m, the mass of the whole disc must be 4m. For complete disc moment of inertia about given axis of mass 4m is given by,
Moment of inertia, =(4M)2R2=2MR2
From the given figure, we can see that the angle made by the cut is 90∘. Therefore, the cut is the perfect quarter of the disc. Hence by symmetry for a given quarter of disc, the moment of inertia of the cut is the quarter of the moment of inertia of the disc. Therefore,
I=42MR2
∴I=21MR2
So, the correct answer is option A.
Additional information:
A measure of the resistance of a body to angular acceleration about a given axis that is equal to the sum of the products of each element of mass in the body and the square of the element’s distance from the axis. When a body is free to rotate around an axis, torque must be applied to change its angular momentum. The amount of torque needed to cause any given angular acceleration is proportional to the moment of inertia of the body. Moment of inertia may be expressed in units of kilogram squared in SI units and pound-foot-second squared imperial or US units. S.I unit of moment of inertia is kg.m2 and Dimensions are ML2.
Note: To answer these type questions, students should remember the moment of inertia of all the often used objects such as disc, ring, rod, etc. Also, the students must be able to determine the moment of inertia using the formula, I=mr2. Note that we have assumed the disc has uniform density.
