Question
Question: One plate of a capacitor is fixed, and the other is connected to the spring as shown in the figure. ...
One plate of a capacitor is fixed, and the other is connected to the spring as shown in the figure. The area of both plates is A. In the steady-state (equilibrium), the separation between the plates is 0.8d (spring has unstretched). The force constant of the spring is approximately
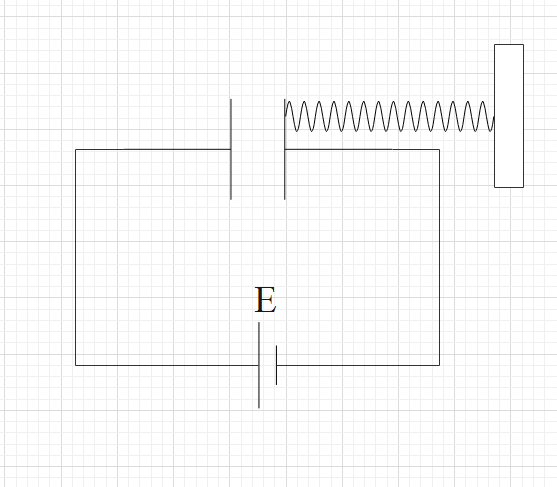
a)32d3125ε0AE2
b) d32ε0AE2
c) Ad36ε0E2
d) d3ε0AE2
Solution
Since we need to find the force constant of spring, so we need the value of force on the spring that is equal to the force on plates due to charged capacitor, i.e. F=2Aε0Q2
Find the value of Q by the formula: Q=CE;C=Dε0A, where D = 0.8d
Then, by using the formula: F=kx, find the value of k for x = 0.2d
Complete step by step answer:
As we know that:
Q=CE, where Q is a charge, C is the capacitance and E is the magnitude of the electric field.
So, substituting the value of C in the above equation, we get:
Q=Dε0AE=0.8dε0AE......(1)
Now, using the formula: F=2Aε0Q2, find the value of force on plates due to charged capacitor, i.e.:
F=2Aε0(0.8dε0AE)2=128d2100ε0AE2......(2)
As we know that force on the spring that is equal to the force on plates due to charged capacitor
Therefore, using the formula: F=kx for x = 0.2d, we get:
⇒128d2100ε0AE2=k(0.2d)⇒k=256d31000ε0AE2⇒k=32d3125ε0AE2
So, the correct answer is “Option A”.
Note:
Derivation of force between two plates of the capacitor:
As we know that, the magnitude of the electric field by anyone plate is: E=2ε0σ=2Aε0Q, where A is the area of the plate.
Also, we know that: ∣F∣=∣Q∣∣E∣
So, we have a force between two plates of the capacitor as:
F=2Aε0Q2
