Question

One of the refracting surfaces of a prism, of refractive index 2 is silvered. The angle of the prism is equal to the critical angle of a medium of refractive index 2. A ray of light incident on the unsilvered surface passes through the prism and retraces its path after reflection at the silvered face. Then the angle of incidence of the unsilvered surface is
(A) $0^\circ$
(B) $30^\circ$
(C) $45^\circ$
(D) $90^\circ$

Answer 1

To find the solution, we will use the relation connecting the critical angle and the refractive index of the prism. We will also use Snell’s law for refraction to reach the final answer.

Complete step by step answer:
Given, the refractive index of the prism, $n = 2$

Let $i$ be the angle of incidence of the light ray at the unsilvered surface and $r$ be the angle of refraction of the ray at the same surface. Also, let $A$ be the angle of the prism.

The light ray incident on the silvered surface $AC$ retraces its path. If a ray incident on a surface retraces its path, then the incident angle of the ray is $90^\circ$.

Now consider the figure below.

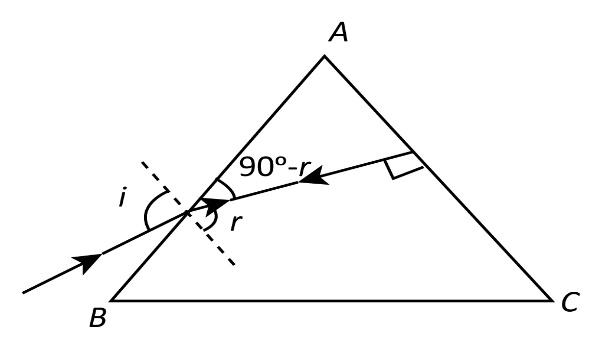
In the figure, we consider $\Delta APQ$. Since the sum of the angles of a triangle is $180^\circ$, we can write

$\left( {90^\circ - r} \right) + A + 90^\circ = 180^\circ \\\ \implies 180^\circ - r + A = 180^\circ \\\ \implies A = r$

Now, the relation connecting critical angle and refractive index of the prism can be written as

$n = \dfrac{1}{{\sin C}}$

where $C$ is a critical angle.

Now, we substitute the value of the refractive index $n$ of the prism in the equation. Then, we get
$\begin{array}{l} 2 = \dfrac{1}{{\sin C}}\\\ \sin C = \dfrac{1}{2} \end{array}$

The sine function has value $\dfrac{1}{2}$ when the angle is $30^\circ$. Therefore,

$C = 30^\circ$

It is given that the angle of prism is equal to the critical angle of a medium of refractive index $2$. Hence, we obtain the angle of the prism $A$ as

$A = 30^\circ$

We obtained earlier that $r = A$, Hence,

$r = 30^\circ$

Now at the silvered surface, we apply Snell’s law. Hence,

$n = \dfrac{{\sin i}}{{\sin r}}$

Since $r = 30^\circ$ and $n = 2$, using the above equation we can write

$2 = \dfrac{{\sin i}}{{\sin 30^\circ }}\\\ \implies 2 = \dfrac{{\sin i}}{{\dfrac{1}{2}}}\\\ \implies 2 = 2\sin i\\\ \implies \sin i = 1$

The sine function has value $1$ when the angle is $90^\circ$. Therefore,
$i = 90^\circ$

So, we get that the angle of incidence of the light ray at the silvered surface is $90^\circ$.

So, the correct answer is “Option D”.

Note:
Snell’s law states that the ratio of the sine of the angle of incidence to the sine of the angle of refraction is equal to the refractive index of the medium. Also, note that the refractive index of a medium is constant irrespective of the angles of incident and refracted rays.