Question
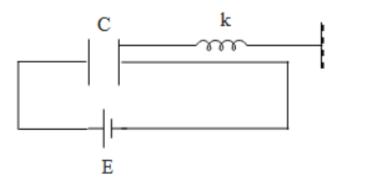
Question: One of the plates of the capacitor is connected to the spring as shown in the figure. Area of both t...
One of the plates of the capacitor is connected to the spring as shown in the figure. Area of both the plates is A. In steady state the separation between the plates is 0.8d(spring was stretched and the distance between the plates was d when the capacitor was uncharged). The force constant of the spring is approximately
a)2d35∈∘AE2b)d22∈∘AEc)Ad36∈∘E2d)2d3∈∘AE2
Solution
In the steady state when the capacitor gets charged completely, both the plates of the capacitor will start attracting each other. As a result it will stretch the spring. Since the restoring force of the spring is equal to the force of attraction between the plates of the capacitor in steady state, we will equate the two and obtain the spring constant.
Formula used:
F(restoring)=−kx
E=2∈∘σ=2∈∘AQ
F(attraction)=EQ
Q=CV
C=dA∈∘
Complete answer:
It is given to us that the initial distance between the plates of the capacitor with area (A) as d, hence the capacitance (C)of the capacitor is given by C=dA∈∘ where ∈∘ is the permittivity of free space.
The charge (Q)on the capacitor is equal to the product of the capacitance (C)times the potential difference (V)across the capacitor. This can be mathematically represented as Q=CV. As the above capacitor gets fully charged when connected to the battery of potential difference E, charge on the capacitor,
Q=C′V⇒Q=dA∈∘E
The force of attraction between the two plates is equal to the product of electric field (E)times the charge on either plate(Q). This can mathematically be represented as F(attraction)=EQ. The electric field (E) between the two positive and negative charged plates is equal to,
E=2∈∘σ, σ=AQ⇒E=2∈∘AQ
Substituting the value of electric field and the charge on the plates in the above expression of force we get,
F(attraction)=EQ⇒F(attraction)=2∈∘AQ2, ∵Q=dA∈∘E⇒F(attraction)=2∈∘A(dA∈∘E)2⇒F(attraction)=d22∈∘AA2∈∘2E2⇒F(attraction)=2d2A∈∘E2
It is given in the question that the capacitor plate is connected to the spring. It is given that the distance between the plates gets reduced to 0.8d. As the initial distance was d, when the spring was not stretched, the extension in the spring is x=d−0.8d=0.2d. The restoring force on the spring is given by F(restoring)=−kx where k is the spring constant and x is the extension in the spring. At equilibrium the force of attraction of the plates will be equal to restoring force of the spring. Therefore after equating them we get,
F(attraction)=F(restoring)2d2A∈∘E2=−kx, since x=0.2d⇒2d2A∈∘E2=−k0.2d⇒k=0.4d3A∈∘E2=2d35∈∘AE2
Hence the correct answer of the above question is option a.
Note:
It is to be noted that one of the plates of the capacitor is taken to be fixed. Hence we could say that one plate i.e. attached to the spring moved by a distance of 0.2d. As a result we could conclude that the extension in spring was also 0.2d.
