Question
Question: One mole of monoatomic real gas satisfies the equation P (V - b) = RT where b is a constant. The rel...
One mole of monoatomic real gas satisfies the equation P (V - b) = RT where b is a constant. The relationship of interatomic potential V (r) and interatomic distance for the gas is given by:
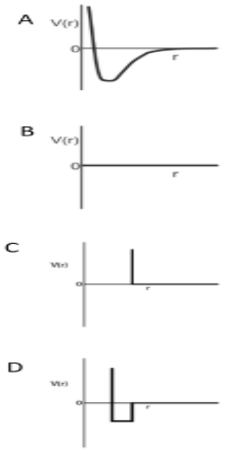
Solution
The Vander Waals equation gives the relationship between pressure, temperature, volume and the amount of gas. The Vander Waal equation gives a relationship for both ideal and real gas with a slight difference.
Complete Step-by-Step Answer:
-As we know that real gas is defined as the gas which occupies the space and also they can interact with other molecules.
-Real gas does not follow ideal gas law that’s why they are also known as non-ideal gas.
-For the real gas, the Vander Waal equation is represented as the
(P + V2an2)(V - nb) = nRT ….. (1)
-Here, P is the pressure, V is the volume and T is the temperature. Whereas a and b are the constant and R is the gas constant.
-The constant 'a' helps in the correction of the intermolecular force whereas 'b' helps in the adjustment of the volume that is occupied by the gas.
-For an ideal gas, the value of a and b constant is equal to the zero and the equation becomes PV = nRT.
-So, for monoatomic gas, the value of n is equal to the 1 but the equation of this gas is given as P(V - b) = RT …….. (2)
-So, by comparing equation first and second, we will observe that the value of a is zero due to which it is constant.
-So, it means that the potential energy will not change as the distance between the molecules changes.
-That’s why for a particular distance it will remain constant but at a certain, the repulsion between the molecules starts.
-And according to this, graph C is the correct answer because firstly it decreases for a particular and starts to decrease.
Therefore, option C is the correct answer.
Note: The Vander Waal equation was given to correct the pressure and volume of the ideal gas and the correction was based on the postulates of Kinetic Theory of Gases. The main advantage of the Vander Waal equation is that it can be used for both gases and liquids.
