Question
Question: One mole of an ideal monoatomic gas is taken round the cyclic process ABCA as shown in figure....
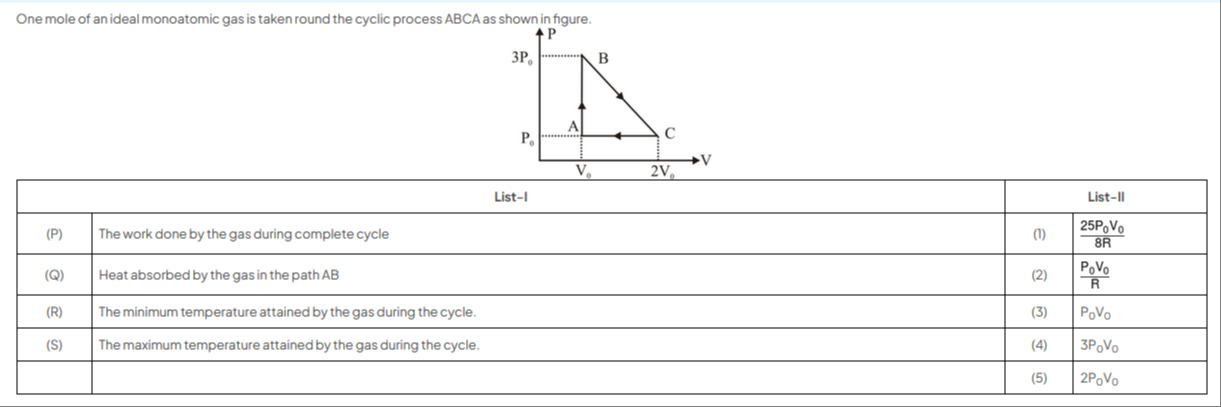
One mole of an ideal monoatomic gas is taken round the cyclic process ABCA as shown in figure.
8R25P0V0
RP0V0
P0V0
3P0V0
2P0V0
P → 3, Q → 4, R → 2, S → 1
Solution
The given cyclic process ABCA for one mole of an ideal monoatomic gas is shown in the P-V diagram. The coordinates of the vertices are A: (V0,P0), B: (V0,3P0), and C: (2V0,P0).
For an ideal gas, PV=nRT. Here n=1, so PV=RT.
(P) The work done by the gas during the complete cycle:
The work done during a cyclic process is the area enclosed by the cycle on the P-V diagram. The cycle ABCA forms a triangle. The vertices are A, B, and C.
The work done is the area of the triangle ABC. The base of the triangle can be taken as the segment CA along the constant pressure line P=P0. The length of the base is VC−VA=2V0−V0=V0.
The height of the triangle is the perpendicular distance from B to the line CA. This is the difference in pressure between B and the line CA (which is at pressure P0), so the height is PB−PA=3P0−P0=2P0.
The area of the triangle is 21×base×height=21×V0×2P0=P0V0.
The cycle is traced in the clockwise direction (A → B → C → A) on the P-V diagram, which means the net work done by the gas is positive.
So, the work done by the gas during the complete cycle is Wcycle=P0V0.
Matching with List-II, (P) corresponds to (3) P0V0.
(Q) Heat absorbed by the gas in the path AB:
Path AB is an isochoric process at volume V0. The pressure changes from P0 to 3P0.
For an isochoric process, the work done is WAB=0.
The change in internal energy is ΔUAB=nCVΔT. For a monoatomic gas, CV=23R.
The temperatures at A and B are TA=RPAVA=RP0V0 and TB=RPBVB=R3P0V0.
ΔUAB=1×23R(TB−TA)=23R(R3P0V0−RP0V0)=23R(R2P0V0)=3P0V0.
According to the first law of thermodynamics, QAB=ΔUAB+WAB.
QAB=3P0V0+0=3P0V0.
Since QAB is positive, heat is absorbed by the gas in the path AB.
Matching with List-II, (Q) corresponds to (4) 3P0V0.
(R) The minimum temperature attained by the gas during the cycle:
The temperature at any point (P,V) is T=RPV.
Temperature at A: TA=RP0V0.
Temperature at B: TB=R3P0V0.
Temperature at C: TC=RP0(2V0)=R2P0V0.
Along path AB (isochoric V=V0), T=RPV0. As P goes from P0 to 3P0, T goes from TA to TB. Minimum temperature is TA.
Along path CA (isobaric P=P0), T=RP0V. As V goes from 2V0 to V0, T goes from TC to TA. Minimum temperature is TA.
Along path BC, the line passes through (V0,3P0) and (2V0,P0). The equation of the line is P−P0=V0−2V03P0−P0(V−2V0)=−V02P0(V−2V0)=−V02P0(V−2V0).
P=P0−V02P0V+4P0=5P0−V02P0V.
The temperature along BC is T(V)=RPV=R1(5P0−V02P0V)V=RP0(5V−V02V2).
To find the minimum temperature, we check the endpoints and any critical points.
T(V0)=RP0(5V0−V02V02)=RP0(5V0−2V0)=R3P0V0=TB.
T(2V0)=RP0(5(2V0)−V02(2V0)2)=RP0(10V0−V024V02)=RP0(10V0−8V0)=R2P0V0=TC.
To find critical points, dVdT=RP0(5−V04V). Setting dVdT=0, we get 5=V04V, so V=45V0.
The second derivative is dV2d2T=RP0(−V04)<0, so this is a maximum.
Thus, the minimum temperature along BC occurs at the endpoints, which are TB and TC.
Comparing the temperatures at the vertices TA=RP0V0, TB=R3P0V0, TC=R2P0V0, the minimum temperature is TA=RP0V0.
Matching with List-II, (R) corresponds to (2) RP0V0.
(S) The maximum temperature attained by the gas during the cycle:
From the previous calculation, the temperatures at the vertices are TA=RP0V0, TB=R3P0V0, TC=R2P0V0.
Along path AB, temperature increases from TA to TB. Maximum is TB.
Along path CA, temperature decreases from TC to TA. Maximum is TC.
Along path BC, the temperature has a maximum at V=45V0.
The maximum temperature along BC is Tmax,BC=T(45V0)=RP0(5(45V0)−V02(45V0)2)=RP0(425V0−V021625V02)=RP0V0(425−1650)=RP0V0(16100−50)=16R50P0V0=8R25P0V0.
Now compare the temperatures TA, TB, TC, and Tmax,BC.
TA=RP0V0=8R8P0V0
TB=R3P0V0=8R24P0V0
TC=R2P0V0=8R16P0V0
Tmax,BC=8R25P0V0.
Comparing these values, the maximum temperature is Tmax,BC=8R25P0V0.
Matching with List-II, (S) corresponds to (1) 8R25P0V0.
Summary of matches:
(P) → (3)
(Q) → (4)
(R) → (2)
(S) → (1)
