Question

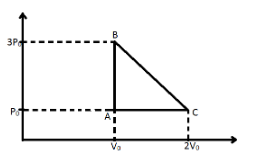
One mole of an ideal monatomic gas is taken along the path ABCA as shown in the PV diagram. The maximum temperature attained by the gas along the path BC is given by:-

A. $\dfrac{{25}}{8}\dfrac{{{P_0}{V_0}}}{R}$
B. $\dfrac{{25}}{4}\dfrac{{{P_0}{V_0}}}{R}$
C. $\dfrac{{25}}{{16}}\dfrac{{{P_0}{V_0}}}{R}$
D. $\dfrac{5}{8}\dfrac{{{P_0}{V_0}}}{R}$

Answer 1

An ideal gas equation is given as $PV = nRT$. We can write the PV equation for the process BC using the equation of straight line $y - {y_1} = \dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}} \left( {x - {x_1}} \right)$, where $\left( {{x_1},{y_1}} \right) and \left( {{x_2},{y_2}} \right)$ are known points B and C. We can convert this PV equation in terms of temperature T using the ideal gas equation. For maximum temperature $\dfrac{{dT}}{{dV}} = 0$.

Complete step by step answer:
We know that an ideal gas equation is given as $PV = nRT$. Therefore temperature $T = \dfrac{{PV}}{{nR}}$.

Given, number of moles, n$= 1$.
Temperature of point A$= \dfrac{{3{P_0}{V_0}}}{R}$
Temperature off point B$= \dfrac{{{P_0}2{V_0}}}{R}$
Now we write the PV equation for the process BC using the equation of a straight line with two given point.
P - 3{P_0} = \dfrac{{{P_0} - 3{P_0}}}{{2{V_0} - {V_0}}}\left( {V - {V_0}} \right) \\\ \Rightarrow P - 3{P_0} = \dfrac{{ - 2{P_0}}}{{{V_0}}}\left( {V - {V_0}} \right) \\\ \Rightarrow P = \dfrac{{ - 2{P_0}V}}{{{V_0}}} + 5{P_0} \\\
Multiplying the equation with $V$.
$PV = \dfrac{{ - 2{P_0}{V^2}}}{{{V_0}}} + 5{P_0}V$
Replacing $PV$ with $RT$.
$RT = - \dfrac{{2{P_0}}}{{{V_0}}}{V^2} + 5{P_0}V$
For maximum temperature $\dfrac{{dT}}{{dV}} = 0$.
Therefore we get the maximum temperature t as
$\therefore T =\dfrac{{25}}{8}\dfrac{{{P_0}{V_0}}}{R}$

Note: It is important to know the equation for ideal gas to solve this question ($PV = nRT$). We find the maximum or minimum value of any quantity using differentiation.For the net work involved in a cyclic process is the area enclosed in a P-V diagram, if the cycle goes clockwise, the system does work and if the cycle goes anticlockwise, then work is done on the system.