Question

One mole of an ideal gas with the adiabatic exponent $\gamma$ goes through the polytropic process as a result of which the absolute temperature of the gas increases $\tau$ fold. The polytropic constant equals $n$. Find the entropy of the gas in this process.
(A) $\dfrac{{(n - \gamma )R}}{{(n - 1)(\gamma - 1)}}\ln \tau$
(B) $\dfrac{{(n - \gamma )R}}{{(n - \gamma )}}\ln \tau$
(C) $\dfrac{{(n - \gamma )R}}{{(n - 1\gamma )(\gamma - 1)}}\ln \tau$
(D) $\dfrac{{(n - \gamma )R}}{{(n - 1)\gamma }}\ln \tau$

Answer 1

Entropy is a term in Physics that is associated with the randomness or disorderness of a particular process. In simple words, it can be explained as the heat or thermal energy that is not useful for any work, per unit temperature.
Formula used:
The formula to calculate entropy is given as
$\int {dS = \int {\dfrac{{dQ}}{T}} }$
Also, the relation between $\;dQ$ and $T$ is given by,
$dQ = nCdT$
For a polytropic process, the formula for molar heat capacity is given as,
$C = \left( {\dfrac{R}{{\gamma - 1}} - \left. {\dfrac{R}{{n - 1}}} \right)} \right.$

Complete step by step solution:
Let the initial temperature be ${T_i}$.
It is given that the absolute temperature increases by $\tau$ fold.
If the final temperature is ${T_f}$ , then we can say that,
${T_f} = \tau {T_i}$

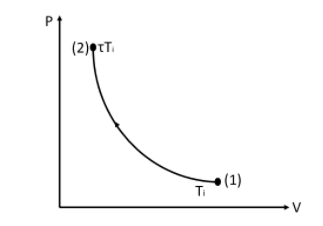
This is the $P - V$ curve for an increase in temperature for an adiabatic process.
From the figure, we can see that the temperature from point $(1)$ has increased to $\tau$ times the initial temperature at point $(2)$.
At point $(2)$ the pressure increases and the volume decreases.
We know that the randomness increases with the decrease in volume.
Therefore we can say that the entropy increases at point $(2)$.
The formula to calculate entropy is given as
$\int {dS = \int {\dfrac{{dQ}}{T}} }$
where, $dS$ is the change in entropy,
$dQ$ is the heat energy released, and
$T$ is the temperature.
$\therefore \Delta S = \int {\dfrac{{dQ}}{T}}$ ……….$(I)$
Also, the relation between $\;dQ$ and $T$ is given by,
$dQ = nCdT$
where, $n$ is the number of moles, and
$C$ is the molar heat capacity.
The value of $C$ can be found using specific heat capacity, or heat capacity per unit mass, $c = \dfrac{C}{m}$.
From the question, we have, $n$ as one mole.
$\therefore dQ = CdT$
Substituting this term in the equation $(I)$ we get,
$\Delta S = \int {\dfrac{{CdT}}{T}}$
According to the requirement of the question, if we integrate the above equation from ${T_i}$ to ${T_f}$ we get, $\Delta S = \int\limits_{{T_i}}^{{T_f}} {\dfrac{{CdT}}{T}}$
Upon solving the integration we get,
$\Delta S = C\left. {\ln T} \right]_{{T_i}}^{{T_f}}$
Substituting the values of the integrating limits we get,
$\Delta S = C(\ln \tau {T_i} - \ln {T_i})$
Using the property of logarithm, $\ln A - \ln B = \ln \dfrac{A}{B}$ we get,
$\Delta S = C\ln \dfrac{{\tau {T_i}}}{{{T_i}}}$
Cancelling ${T_i}$ from numerator and denominator we get,
$\Delta S = C\ln \tau$ ……….$(II)$
For a polytropic process, the formula for molar heat capacity is given as,
$C = \left( {\dfrac{R}{{\gamma - 1}} - \left. {\dfrac{R}{{n - 1}}} \right)} \right.$
where, $n$ is given in the question as the polytropic constant,
$R$ is the Rydberg’s constant, and
$\gamma$ is the adiabatic exponent.
Substituting this value in the equation $(II)$ we get,
$\Delta S = \left( {\dfrac{R}{{\gamma - 1}} - \left. {\dfrac{R}{{n - 1}}} \right)} \right.\ln \tau$
Taking $R$ common,
$\Delta S = R\left( {\dfrac{1}{{\gamma - 1}} - \left. {\dfrac{1}{{n - 1}}} \right)} \right.\ln \tau$
$\Rightarrow \Delta S = R\left[ {\dfrac{{(n - 1) - (\gamma - 1)}}{{(n - 1)(\gamma - 1)}}} \right]\ln \tau$
Upon solving the numerator we get,
$\Delta S = R\left[ {\dfrac{{n - \gamma }}{{(n - 1)(\gamma - 1)}}} \right]\ln \tau$
$\Rightarrow \Delta S = \dfrac{{(n - \gamma )R}}{{(n - 1)(\gamma - 1)}}\ln \tau$

Hence the correct answer is option (A) $\dfrac{{(n - \gamma )R}}{{(n - 1)(\gamma - 1)}}\ln \tau$.

Note: The adiabatic exponent, or the heat capacity ratio, or Laplace’s coefficient $\gamma$ is equal to the ratio between the heat capacity at constant pressure, ${C_P}$ and the heat capacity at constant volume, ${C_V}$. This concept is specially applied for processes involving ideal gases.