Question

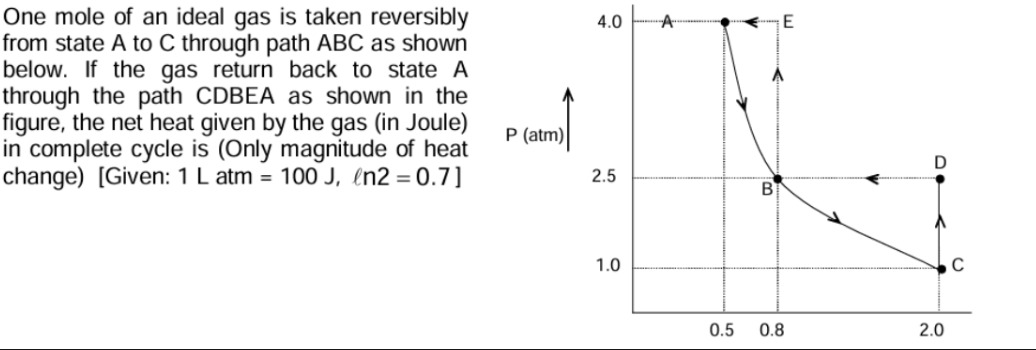
One mole of an ideal gas is taken reversibly from state A to C through path ABC as shown below. If the gas return back to state A through the path CDBEA as shown in the figure, the net heat given by the gas (in Joule) in complete cycle is (Only magnitude of heat change) [Given: 1 L atm = 100 J, $\ln2 = 0.7$]

Answer 1

140

Answer 2

The cycle is A $\to$ C through path ABC, and then C $\to$ A through path CDBEA. The net heat given by the gas in a complete cycle is equal to the net work done by the gas in the cycle, i.e., $Q_{cycle} = W_{cycle}$. The net work done in the cycle is the sum of the work done in each process. $W_{cycle} = W_{ABC} + W_{CDBEA}$.

First, let's find the work done in path ABC. From the figure, the points A, B, and C have coordinates: A: (V=0.5 L, P=4.0 atm) B: (V=0.8 L, P=2.5 atm) C: (V=2.0 L, P=1.0 atm) Let's check the product PV for these points: $P_A V_A = 4.0 \text{ atm} \times 0.5 \text{ L} = 2.0 \text{ L atm}$ $P_B V_B = 2.5 \text{ atm} \times 0.8 \text{ L} = 2.0 \text{ L atm}$ $P_C V_C = 1.0 \text{ atm} \times 2.0 \text{ L} = 2.0 \text{ L atm}$ Since $PV$ is constant along the path ABC, the path ABC is an isothermal process. The work done in an isothermal process for an ideal gas is given by $W = \int_{V_i}^{V_f} P dV$. Since $PV = \text{constant} = 2.0$, $P = \frac{2.0}{V}$. $W_{ABC} = \int_{V_A}^{V_C} \frac{2.0}{V} dV = 2.0 [\ln V]_{V_A}^{V_C} = 2.0 (\ln V_C - \ln V_A) = 2.0 \ln(\frac{V_C}{V_A})$. $W_{ABC} = 2.0 \ln(\frac{2.0}{0.5}) = 2.0 \ln(4) = 2.0 \times 2 \ln(2) = 4.0 \ln(2)$. Given $\ln 2 = 0.7$, $W_{ABC} = 4.0 \times 0.7 = 2.8 \text{ L atm}$. Converting to Joules, $W_{ABC} = 2.8 \text{ L atm} \times 100 \frac{\text{J}}{\text{L atm}} = 280 \text{ J}$.

Next, let's find the work done in path CDBEA. This path consists of four segments: C to D, D to B, B to E, and E to A. The coordinates of the points are: C: (V=2.0 L, P=1.0 atm) D: (V=2.0 L, P=2.5 atm) B: (V=0.8 L, P=2.5 atm) E: (V=0.8 L, P=4.0 atm) A: (V=0.5 L, P=4.0 atm)

Path C to D: Isochoric process (constant volume, V=2.0 L). $W_{CD} = \int_{V_C}^{V_D} P dV = 0$ since $dV=0$. Path D to B: Isobaric process (constant pressure, P=2.5 atm). $W_{DB} = \int_{V_D}^{V_B} P dV = P (V_B - V_D) = 2.5 \text{ atm} \times (0.8 - 2.0) \text{ L} = 2.5 \times (-1.2) \text{ L atm} = -3.0 \text{ L atm}$. Path B to E: Isochoric process (constant volume, V=0.8 L). $W_{BE} = \int_{V_B}^{V_E} P dV = 0$ since $dV=0$. Path E to A: Isobaric process (constant pressure, P=4.0 atm). $W_{EA} = \int_{V_E}^{V_A} P dV = P (V_A - V_E) = 4.0 \text{ atm} \times (0.5 - 0.8) \text{ L} = 4.0 \times (-0.3) \text{ L atm} = -1.2 \text{ L atm}$.

The total work done in path CDBEA is $W_{CDBEA} = W_{CD} + W_{DB} + W_{BE} + W_{EA} = 0 + (-3.0) + 0 + (-1.2) = -4.2 \text{ L atm}$. Converting to Joules, $W_{CDBEA} = -4.2 \text{ L atm} \times 100 \frac{\text{J}}{\text{L atm}} = -420 \text{ J}$.

The net work done in the cycle is $W_{cycle} = W_{ABC} + W_{CDBEA} = 280 \text{ J} + (-420) \text{ J} = -140 \text{ J}$. The net heat given by the gas in the complete cycle is $Q_{cycle} = W_{cycle} = -140 \text{ J}$. The negative sign indicates that the net heat is given out by the gas. The question asks for the magnitude of the net heat given by the gas. Magnitude of heat change = $|-140 \text{ J}| = 140 \text{ J}$.