Question

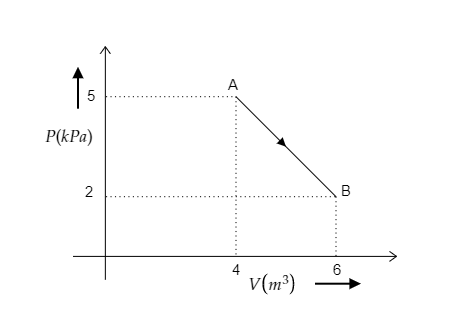
One mole of an ideal diatomic gas undergoes a transition from A to B along a path AB as shown in the figure. Find the change in internal energy of the gas during the transition.

A) $- 20{\text{kJ}}$
B) $20{\text{J}}$
C) $- 12{\text{kJ}}$
D) $20{\text{kJ}}$

Answer 1

The change in internal energy of one mole of an ideal diatomic gas depends on its molar specific heat capacity at constant volume and change in temperature of the gas along the path AB If the temperature decreases along the path the internal energy will also decrease. The ideal gas equation gives the temperature at a point in terms of the pressure and volume of the gas at that point.

Formulas used:
The ideal gas equation is given by, $PV = nRT$ where $P$ is the pressure of the gas, $V$ is its volume, $n$ is the number of moles present in the gas and $R$ is the gas constant.
The change in internal energy of a gas is given by, $\Delta U = n{C_V}\Delta T$ where $n$ is the number of moles present in the gas, ${C_V}$ is the molar specific heat of the gas at constant volume and $\Delta T$ is the change in temperature of the gas.

Complete step by step answer:
Step 1: List the pressure and volume of the gas from the given figure.
The figure representing the variation of pressure of the gas with its volume along a path AB is given below.

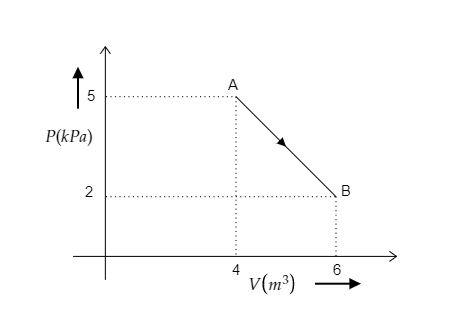
In the above figure, the ideal gas undergoes a transition from point A to point B.
The initial pressure of the gas is the pressure at A and it is given to be ${P_1} = 5{\text{kPa}} = 5 \times {10^3}{\text{Pa}}$.
The initial volume of the gas is the volume at A and it is given to be ${V_1} = 4{{\text{m}}^3}$.
Similarly, the final pressure and volume of the gas for the path AB will be the pressure and volume at B.
i.e., ${P_2} = 2{\text{kPa}} = 2 \times {10^3}{\text{Pa}}$ and ${V_2} = 6{{\text{m}}^3}$.
The number of moles present in the ideal gas is mentioned as $n = 1$.
Step 2: Using the ideal gas equation, express the temperature of the gas at A and B and then calculate the change in temperature along the path.
The ideal gas equation for one mole of an ideal gas is given by, $PV = RT$ where $P$ is the pressure of the gas, $V$ is its volume and $R$ is the gas constant.
From the above equation, the temperature of the gas can be expressed as $T = \dfrac{{PV}}{R}$
Then the initial temperature of the path AB will be ${T_1} = \dfrac{{{P_1}{V_1}}}{R}$ ---------- (1)
Substituting the values for ${P_1} = 5{\text{kPa}}$ and ${V_1} = 4{{\text{m}}^3}$ in equation (1) we get, ${T_1} = \dfrac{{5 \times {{10}^3} \times 4}}{R} = \dfrac{{20 \times {{10}^3}}}{R}$
Thus the temperature at A is ${T_1} = \dfrac{{20 \times {{10}^3}}}{R}$.
The final temperature of the path AB will be ${T_2} = \dfrac{{{P_2}{V_2}}}{R}$ ---------- (2)
Substituting the values for ${P_2} = 2{\text{kPa}}$ and ${V_2} = 6{{\text{m}}^3}$ in equation (2) we get,
$\Rightarrow {T_2} = \dfrac{{2 \times {{10}^3} \times 6}}{R} = \dfrac{{12 \times {{10}^3}}}{R}$
Thus the temperature at B is
$\Rightarrow {T_2} = \dfrac{{12 \times {{10}^3}}}{R}$.
Then the change in temperature is $\Delta T = {T_2} - {T_1}$
Substituting the values for ${T_1} = \dfrac{{20 \times {{10}^3}}}{R}$ and ${T_2} = \dfrac{{12 \times {{10}^3}}}{R}$ in the above relation we get,
$\Rightarrow \Delta T = \left( {\dfrac{{12 \times {{10}^3}}}{R}} \right) - \left( {\dfrac{{20 \times {{10}^3}}}{R}} \right)$
On simplifying we get the change in temperature as
$\Rightarrow \Delta T = \dfrac{{ - 8 \times {{10}^3}}}{R}$
Step 3: Express the relation to find the change in the internal energy of the gas along the path.
The change in internal energy of a gas is given by, $\Delta U = n{C_V}\Delta T$
where $n$ is the number of moles present in the gas, ${C_V}$ is the molar specific heat of the gas at constant volume and $\Delta T$ is the change in temperature of the gas.
For a diatomic gas, the molar specific heat capacity at constant volume is
$\Rightarrow {C_V} = \dfrac{{5R}}{2}$.
Then the change in internal energy of one mole of an ideal diatomic gas along the path AB will be
$\Rightarrow \Delta U = \dfrac{{5R}}{2}\Delta T$ --------- (3)
Substituting for $\Delta T = \dfrac{{ - 8 \times {{10}^3}}}{R}$ in equation (3) we get,
$\Rightarrow \Delta U = \dfrac{{5R}}{2} \times \dfrac{{ - 8 \times {{10}^3}}}{R} = - 20{\text{kJ}}$

Thus the change in internal energy during the transition is $\Delta U = - 20{\text{kJ}}$. So the correct option is A.

Note:
The molar specific heat of a gas at constant volume depends on the degree of freedom $f$ of the gas. The degree of freedom refers to the number of ways in which the atoms can move. The movement can be rotational or translational. For a diatomic gas, the degree of freedom is 5 and hence ${C_V} = \dfrac{{fR}}{2} = \dfrac{{5R}}{2}$. The negative sign indicates that the internal energy of the gas has decreased along the path.