Question

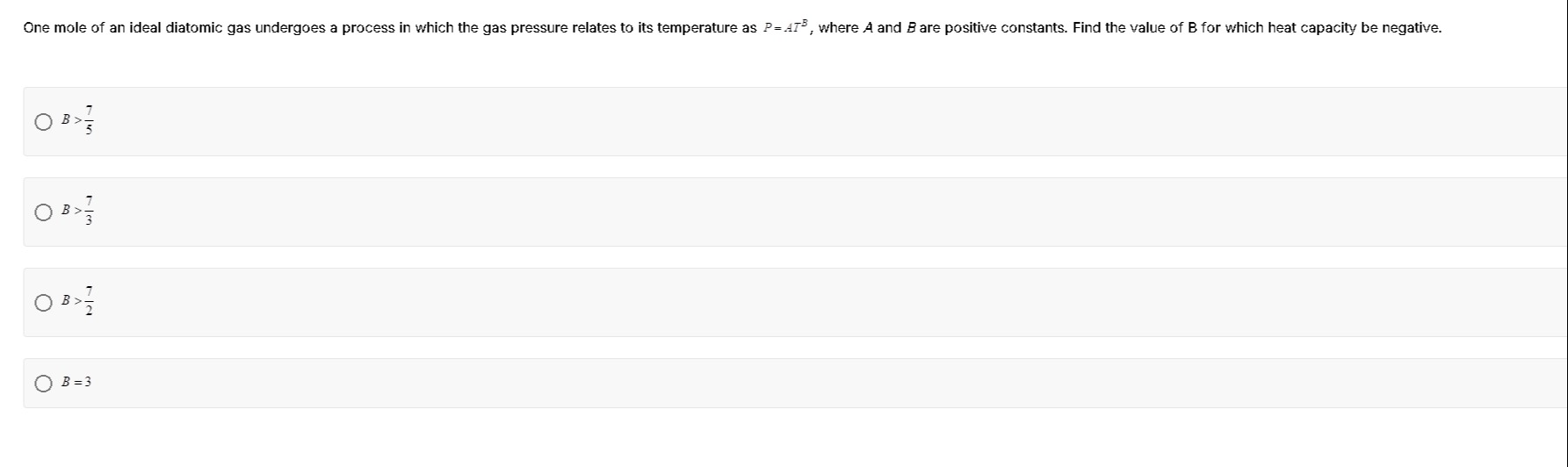
One mole of an ideal diatomic gas undergoes a process in which the gas pressure relates to its temperature as $P = AT^B$, where $A$ and $B$ are positive constants. Find the value of $B$ for which heat capacity be negative.

• A. $B>\frac{7}{5}$
• B. $B>\frac{7}{3}$
• C. $B>\frac{7}{2}$
• D. $B=3$

Answer 1

Answer: (C)

$B>\frac{7}{2}$

Answer 2

For one mole of an ideal diatomic gas, the internal energy change is

$$dU = C_V\,dT = \frac{5}{2}R\,dT.$$

Using the ideal gas law $PV = RT$ and given $P = A T^B$, we obtain

$$V = \frac{RT}{P} = \frac{R}{A}\,T^{1-B}.$$

Differentiate with respect to $T$:

$$dV = \frac{R}{A}(1-B)T^{-B}\,dT.$$

Thus, the work done is

$$dW = P\,dV = A T^B \cdot \frac{R}{A}(1-B)T^{-B}\,dT = R(1-B)\,dT.$$

The heat added is

$$dQ = dU + dW = \left(\frac{5}{2}R + R(1-B)\right)dT = R\left(\frac{7}{2} - B\right)dT.$$

The effective heat capacity for the process is

$$C = \frac{dQ}{dT} = R\left(\frac{7}{2} - B\right).$$

For the heat capacity to be negative,

$$\frac{7}{2} - B < 0 \quad \Longrightarrow \quad B > \frac{7}{2}.$$