Question

One mole of an ideal diatomic gas is taken through the cycle as shown in the figure:
$1 \to 2$: isochoric process
$2 \to 3$: a straight line of P-V diagram
$3 \to 1$: isobaric process

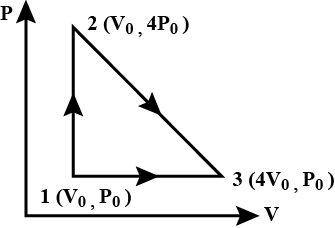
The average molecular speed of the gas in the states 1, 2 and 3 in the ratio:

A. $1:2:2$
B. $1:\sqrt 2 :\sqrt 2$
C. $1:1:1$
D. $1:2:4$

Answer 1

In $1 \to 2$, Pressure is directly proportional to temperature. In $3 \to 1$, Volume is directly proportional to Temperature. And the average molecular speed $\left( {{V_{rms}}} \right)$ is directly proportional to $\sqrt {\dfrac{{RT}}{M}}$, hence $v \propto \sqrt T$​

Complete step by step answer:
In the state 1
Let temperature be ${T_o}$
and we know that, $PV = nRT$
In the state 2
Since $1 \to 2$ is an isochoric process
Hence, in State 1
$\dfrac{P}{T} =$ Constant
$v \propto {T_0}$ ​
when Pressure is equal to $4{P_o}$. Thus, the Temperature $= 4{T_o}$​

State 3
Since $3 \to 1$ is an isobaric process,
According to Charlee’s law
$V \propto T$
$\dfrac{V}{T} =$ Constant
When Volume is $4{V_o}$. Thus Temperature $= 4{T_o}$

The root-mean-square speed or the average molecular speed $\left( {{V_{rms}}} \right)$ is directly proportional to $\sqrt {\dfrac{{RT}}{M}}$
$\Rightarrow v \propto \sqrt T$​
The average velocity of the gas molecule has the formula : ​${V_{avg}} = \sqrt {\dfrac{{8RT}}{M}}$
Where,
V= molecular speed of the particle
T = Temperature in Kelvin
M = molar mass of the compound
R = Ideal gas constant

Hence,
State 1, $v \propto {T_0}$​
State 2, $v \propto \sqrt {4{T_o}} = 2\sqrt {{T_o}}$
State3, $v \propto \sqrt {4{T_o}} = 2\sqrt {{T_o}}$
Hence, ${V_1}:{V_2}:{V_3} = \sqrt {{T_o}} :\sqrt {4{T_o}} :\sqrt {4Y{T_o}}$
Ratio $= 1:2:2$

Therefore, the correct answer is option (A).

Note: Isobaric process is carried out at a constant pressure. In such a process $dP = 0$. Isochoric process is a process in which the volume of the system remains constant, whereby $dV = 0$. According to the Kinetic Molecular Theory of Gases, the molecular speed of the gas explains that gas particles are in continuous motion and they exhibit ideally elastic collisions.