Question

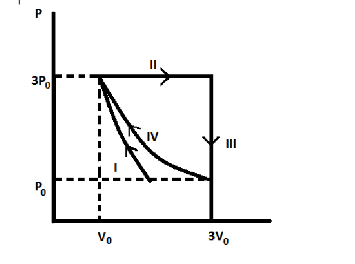
One mole of a monatomic ideal gas undergoes four thermodynamic processes as shown schematically in the PV- diagram below. Among these four processes, one is isobaric, one is isochoric, one is isothermal and one is adiabatic. Match the processes mentioned in list-I with the corresponding statements in list-II.

List -I	List -II
P. In process	1. Work done by the gas is zero
Q. In process II	2. Temperature of the gas remains unchanged
R. In process III	No heat is exchanged between the gas and its surroundings
S. In process IV	4. Work done by the gas is $6{p_0}{v_0}$

A) $P \to 4;Q \to 3;R \to 1;S \to 2$
B) $P \to 1;Q \to 3;R \to 2;S \to 4$
C) $P \to 3;Q \to 4;R \to 1;S \to 2$
D) $P \to 3;Q \to 4;R \to 2;S \to 1$

Answer 1

The thermal behavior of a system is described in terms of thermodynamic variables. For an ideal gas, these variables are pressure, volume, temperature, and number of moles or moles of the gas. According to these variables we will state the thermodynamic processes, by which we will determine the match for the processes mentioned in list-I with the corresponding statements in list-II.

Complete step-by-step solution:
$\to$ From the thermodynamic process shown, Process I is an adiabatic process.
It is a type of process which occurs without transferring of heat or mass between the system and its surrounding. It transfers energy to the surroundings only as work.
Therefore, $\Delta Q = \Delta U + \Delta W$
Now, $\Delta Q = 0$
Therefore, $W = - \Delta U$
Now, volume of gas is decreasing, then $W < 0$ and $\Delta U > 0$
Then, the temperature of the gas increases and no heat is exchanged between the gas and the surrounding.
$\to$ From thermodynamics, Process II is an isobaric process.
It is a type of process where pressure remains constant, so $W = P\Delta V = 3{P_0}\left[ {3{V_0} - {V_0}} \right] = 6{P_0}{V_0}$
$\to$ From thermodynamics, Process III is an Isochoric process.
It is a type of process where volume remains constant, so $\Delta Q = \Delta U + W$
Work done by the gas,$\Delta W = 0$
Therefore, $\Delta Q = \Delta U$
$\to$ From thermodynamics, Process IV is an Isothermal process.
It is a type of process where temperature remains constant.
Therefore, $\Delta Q = \Delta U + \Delta W$
$\Rightarrow$ $\Delta U = 0$
Hence, option C)$P \to 3;Q \to 4;R \to 1;S \to 2$ is the correct answer.

Note: In this question, we need a good knowledge about the processes in thermodynamics that helps us to solve these types of questions easily. Remember that, in adiabatic, no heat is exchanged between the systems. In isobaric, the system's pressure is constant. In isochoric, the system's volume is constant. And in isothermal, the system's temperature is constant.