Question

One mole of a monatomic ideal gas goes through a thermodynamic cycle, as shown in the volume versus temperature $\left( {V - T} \right)$ diagram. The correct statement(s) is/are? [$R$ is the gas constant]

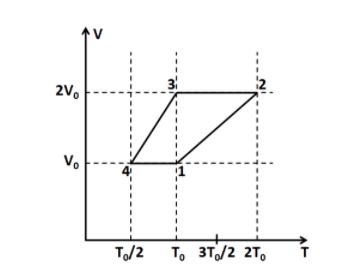
(A) Work done in this thermodynamic cycle $\left( {1 \to 2 \to 3 \to 4 \to 1} \right)$ is $\left| W \right| = \dfrac{1}{2}R{T_0}$
(B) The ratio of heat transfer during processes $1 \to 2$ and $2 \to 3$ is $\left| {\dfrac{{{Q_{1 \to 2}}}}{{{Q_{2 \to 3}}}}} \right| = \dfrac{5}{3}$
(C) The above the thermodynamic cycle exhibits only isobaric and adiabatic processes
(D) The ratio of heat transfer during processes $1 \to 2$ and $3 \to 4$ is $\left| {\dfrac{{{Q_{1 \to 2}}}}{{{Q_{3 \to 4}}}}} \right| = \dfrac{1}{2}$

Answer 1

To solve this question, we need to identify each of the four processes in the given T-V diagram. Then we have to use the standard formulae for the work done and the heat transferred for the respective processes.

Complete step-by-step solution:
For process $1 \to 2$:
This process is represented by a straight line in the given V-T diagram. We know that the slope of a straight line is constant.
We know from the ideal gas equation that
$PV = nRT$
$V = \dfrac{{nR}}{P}T$
Comparing with the equation of a line $y = mx$, we get the slope of the line representing the process $1 \to 2$ as
$m = \dfrac{{nR}}{P}$
Since the slope is constant, so $\dfrac{{nR}}{P}$ is also a constant. Now, the quantity of the gas doesn’t change during the cycle, so the number of moles $n$ remains constant. This means that in this process the pressure $P$ is constant.
Now, substituting the values of the state
So the process $1 \to 2$ is an isobaric process.
For process $2 \to 3$:
This process is represented by a horizontal line in the given T-V diagram. So this means that the volume is constant in this process.
So the process $2 \to 3$ is an isochoric process.
Similarly we can show that the processes $3 \to 4$ and $4 \to 1$ are isobaric and isochoric, respectively.
Thus, the above thermodynamic cycle exhibits only isobaric and isochoric processes.
Hence, the option C is incorrect.
Now, we know that the work done in an isobaric process is given by
$W = nR\Delta T$
According to the question, we have one mole of gas. Therefore we have
$W = R\Delta T$.....................(1)
So the work done in the process $1 \to 2$ is given by
${W_{1 \to 2}} = R\left( {{T_2} - {T_1}} \right)$
From the given diagram, ${T_2} = 2{T_0}$, and ${T_1} = {T_0}$. Substituting these above we get
$\Rightarrow$ ${W_{1 \to 2}} = R{T_0}$......................(2)
Also from (1) the work done in the process $3 \to 4$ is given by
${W_{3 \to 4}} = R\left( {{T_4} - {T_3}} \right)$
From the given diagram, ${T_3} = {T_0}$, and ${T_4} = {T_0}/2$. Substituting these above we get
$\Rightarrow$ ${W_{1 \to 2}} = - \dfrac{1}{2}R{T_0}$.......................(3)
Now, we know that the work done in an isochoric process is equal to zero. Therefore we have
$\Rightarrow$ ${W_{2 \to 3}} = 0$..........................(4)
$\Rightarrow$ ${W_{4 \to 1}} = 0$...............................(5)
The net work done in the complete cycle is
$\Rightarrow$ $W = {W_{1 \to 2}} + {W_{2 \to 3}} + {W_{3 \to 4}} + {W_{4 \to 1}}$
Putting (2) (3) (4) and (5) above, we get
$\Rightarrow$ $W = R{T_0} + 0 - \dfrac{1}{2}R{T_0} + 0$
$\Rightarrow W = \dfrac{1}{2}R{T_0}$
Thus, the work done in the complete cycle is $\left| W \right| = \dfrac{1}{2}R{T_0}$.
Hence, the option A is correct.
Now, we know that the heat transfer in an isobaric process is given by
$\Rightarrow$ $Q = n{C_P}\Delta T$
Since there in one mole of gas, so we have
$\Rightarrow$ $Q = {C_P}\Delta T$
So the heat transfer the process $1 \to 2$ is
$\Rightarrow$ ${Q_{1 \to 2}} = {C_P}\left( {{T_2} - {T_1}} \right)$
Substituting ${T_2} = 2{T_0}$, and ${T_1} = {T_0}$ we get
$\Rightarrow$ ${Q_{1 \to 2}} = {C_P}{T_0}$....................................(6)
Similarly the heat transfer in the process $3 \to 4$ is
${Q_{3 \to 4}} = - {C_P}\dfrac{{{T_0}}}{2}$..........................(7)
Also, we know that the work done in an isochoric process is given by
$Q = n{C_v}\Delta T$
Since there in one mole of gas, so we have
$Q = {C_v}\Delta T$
So the heat transfer the process $2 \to 3$ is
${Q_{2 \to 3}} = {C_v}\left( {{T_3} - {T_2}} \right)$
Substituting ${T_2} = 2{T_0}$, and ${T_3} = {T_0}$ we get
${Q_{2 \to 3}} = - {C_v}{T_0}$ ………………………..(8)
Similarly, the heat transfer in the process $4 \to 1$ is
${Q_{4 \to 1}} = \dfrac{1}{2}{C_v}{T_0}$ …….(9)
Dividing (6) by (8) we get
$\Rightarrow$ $\dfrac{{{Q_{1 \to 2}}}}{{{Q_{2 \to 3}}}} = \dfrac{{{C_P}{T_0}}}{{ - {C_v}{T_0}}}$
$\Rightarrow$ $\dfrac{{{Q_{1 \to 2}}}}{{{Q_{2 \to 3}}}} = - \dfrac{{{C_P}}}{{{C_v}}}$
We know that $\dfrac{{{C_P}}}{{{C_v}}} = \gamma$, and for a monatomic gas, we have $\gamma = \dfrac{5}{3}$. Therefore we have
$\Rightarrow$ $\dfrac{{{Q_{1 \to 2}}}}{{{Q_{2 \to 3}}}} = - \dfrac{5}{3}$
Taking modulus both sides, we get
$\Rightarrow$ $\left| {\dfrac{{{Q_{1 \to 2}}}}{{{Q_{2 \to 3}}}}} \right| = \dfrac{5}{3}$
Therefore, the option B is correct.
Now, dividing (6) by (7) we have
$\Rightarrow$ $\dfrac{{{Q_{1 \to 2}}}}{{{Q_{3 \to 4}}}} = \dfrac{{{C_P}{T_0}}}{{ - {C_p}{T_0}/2}}$
$\dfrac{{{Q_{1 \to 2}}}}{{{Q_{3 \to 4}}}} = - 2$
Taking modulus both sides, we get
$\Rightarrow$ $\left| {\dfrac{{{Q_{1 \to 2}}}}{{{Q_{3 \to 4}}}}} \right| = 2$
Therefore, option D is incorrect.

Hence, the correct options are A and B.

Note: We could also attempt this question by obtaining the P-V diagram from the given T-S diagram. From there we could have directly got the value of the net work done in the cycle by calculating the area of the loop.