Question

One mapping is selected at random from all mappings of the set $S = \\{ 1,2,3,....,n\\}$ into itself. If the probability that mapping is one-one is $\dfrac{3}{{32}}$ then the value of n is ?
A) 2
B) 3
C) 4
D) None of these

Answer 1

A relation $\mathbb{R}:{\text{ A}} \to {\text{B}}$is defined as a function if every element of set A is mapped to one element of set B, i.e. , each object has only one image.

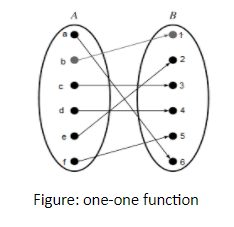
One-one function: When each element of set B is mapped to only one element of set A, i.e., each object in set A has a unique image in set B, then the function is called one-one function.
Let the number of elements in set A = n(A) = a
The number of elements in set B = n(B) = b
Necessary condition : ${\text{b }} \geqslant {\text{ a}}$ [ for one-one function $f:{\text{ A}} \to {\text{B}}$] …… (1)
Total number of functions $= \mathop {\text{b}}\nolimits^{\text{a}}$ …… (2)
Number of one-one functions $= C({\text{b,a)}} \cdot {\text{a!}}$ $(\because 'C'{\text{is combination)}}$ …… (3)

Complete step by step solution:
The mapping of set $S = \\{ 1,2,3,....,n\\}$ into itself can be drawn as,

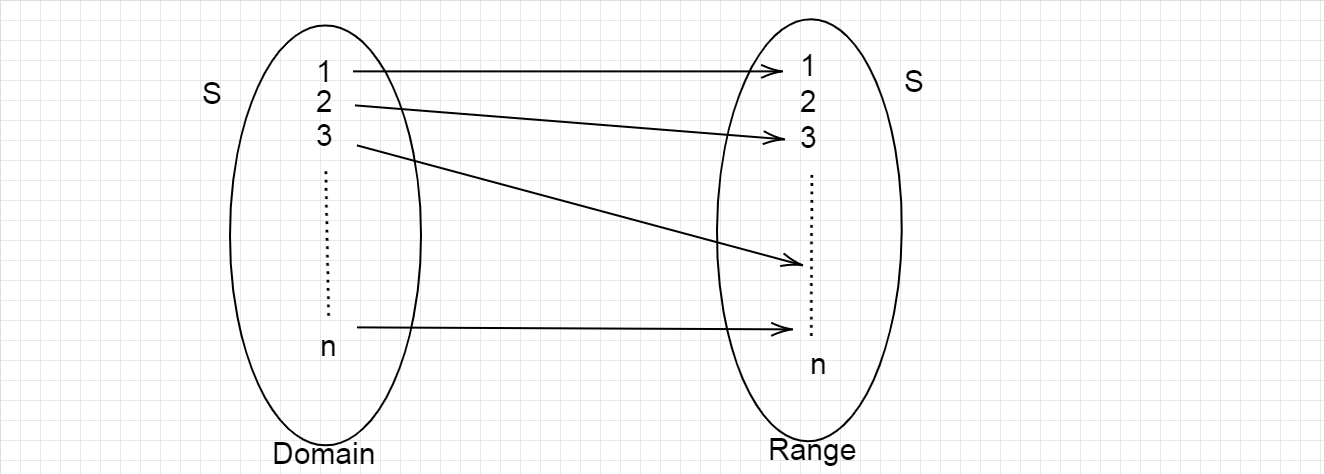
Where the image of every element $x$ in the domain, there exists an element $f(x)$ in the range.

Step 1
Given set $S = \\{ 1,2,3,....,n\\}$

Step 2
Function $f:{\text{ S}} \to {\text{S}}$is defined. $(\because {\text{given}})$

Step 3
Number of elements in set S = n(S) = n.
Total number of functions $f:{\text{ S}} \to {\text{S = }}\mathop {{\text{ }}n}\nolimits^n$ (from (2)) …… (4)

Step 4
Number of one-one functions $f:{\text{S}} \to {\text{S = }}C({\text{n,n)}}{\text{.n}}!$ (from (3))
$= {\text{n!}}$ …… (5)

Step 5
Probability (selecting mapping is one-one) = $\dfrac{{{\text{number of one - one functions }}f:{\text{S}} \to {\text{S }}\;}}{{{\text{total number of functions }}f:{\text{S}} \to {\text{S}}}} = \dfrac{3}{{32}}$
$(\because {\text{given}})$
$= \dfrac{{{\text{n!}}}}{{\mathop {\text{n}}\nolimits^{\text{n}} }} = \dfrac{3}{{32}}$ (from (4) and (5)) $\therefore$ n = 4 [by inspection]

Therefore, the correct option is (C), n=4.

Note:
Another classification of functions is onto functions. If for functions $f:{\text{A}} \to {\text{B}}$the co-domain set of B is also the range for the function, then the function is called an onto function.
The functions which are both one-one and onto are called bijective functions.