Solveeit Logo
Login

Question

Question: One line forms two regions in a plane. Similarly, two lines in a plane can form a maximum of four re...

One line forms two regions in a plane. Similarly, two lines in a plane can form a maximum of four regions. These are shown in the figures.


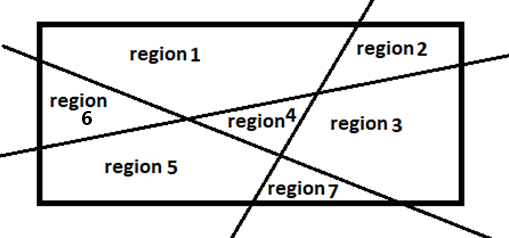
What is the maximum number of regions that can be formed by 4 lines in a plane? Lines need not be concurrent.
A.7
B.8
C.10
D.11

Explanation

Solution

At first we have given that One line forms two regions in a plane and two lines in a plane can form a maximum of four regions, similarly, we’ll find for the maximum number of regions for three lines.
From there we’ll get a particular type of series to easily determine the maximum regions made by four lines.

Complete step-by-step answer:
Given data: One line forms two regions in a plane
Two lines in a plane can form a maximum of four regions
Let's say that f(n)f\left( n \right) is the function resulting in the maximum regions that can be formed in a plane when n lines are there.
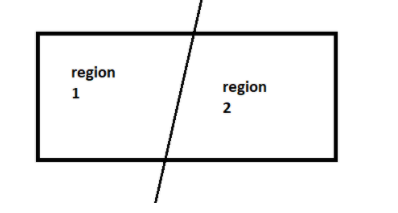
Now we know that one line forms 2 regions in a plane i.e.

Therefore, f(1)=2f(1) = 2
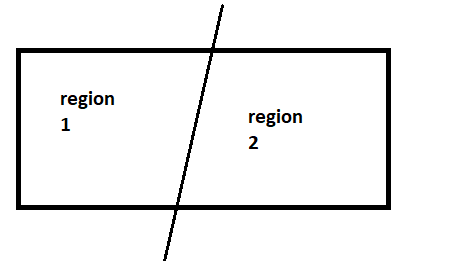
Similarly, it is given that two lines in a plane can form a maximum of four regions

Therefore, f(2)=4f(2) = 4
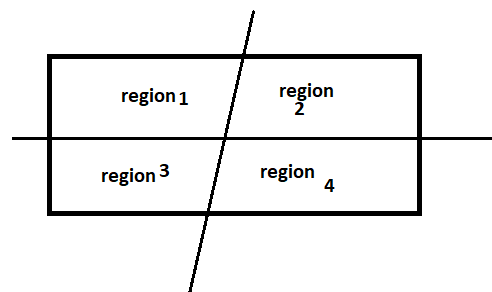
Similarly, we can check for three lines

Therefore, three lines in a plane can form a maximum of seven regions
Therefore, f(3)=7f(3) = 7
From the value of f(1), f(2),f\left( 1 \right),{\text{ }}f\left( 2 \right),and f(3)f\left( 3 \right) we can conclude that as the nth{n^{th}} is include the maximum region increases by ‘n’
That is f(3)=f(2)+3f(3) = f(2) + 3
⇒f(3)=4+3=7\Rightarrow f(3) = 4 + 3 = 7
Therefore, f(4)=f(3)+4f(4) = f(3) + 4
On substituting the value of f(3)f\left( 3 \right) we get,
⇒f(4)=7+4\Rightarrow f(4) = 7 + 4
∴f(4)=11\therefore f(4) = 11
Therefore the required number of regions is 11.
Option(D) is correct.

Note: We can also proof the above solution as we found that
f(1)=2f(1) = 2 , f(2)=4f(2) = 4 and f(3)=7f(3) = 7
We can say that the no lines include we have one area as a whole
i.e. f(0)=1f(0) = 1
Now f(1)−f(0)=1f(1) - f(0) = 1
f(2)−f(1)=2f(2) - f(1) = 2
f(3)−f(2)=3f(3) - f(2) = 3
.
.
.
f(n)−f(n−1)=nf(n) - f(n - 1) = n
Adding all the above equations
⇒f(n)−f(0)=1+2+3+4........+n\Rightarrow f(n) - f(0) = 1 + 2 + 3 + 4........ + n
Now we know that sum of first n natural numbers is given by n(n+1)2\dfrac{{n(n + 1)}}{2}
⇒f(n)−1=n(n+1)2\Rightarrow f(n) - 1 = \dfrac{{n(n + 1)}}{2}
Adding 1 on both sides
⇒f(n)=n(n+1)2+1\Rightarrow f(n) = \dfrac{{n(n + 1)}}{2} + 1
Now substituting n=4n = 4
⇒f(4)=4(5)2+1\Rightarrow f(4) = \dfrac{{4(5)}}{2} + 1
=10+1= 10 + 1
=11= 11, which gives a similar answer as the above solution.