Question

One Indian and four American men and their wives are to be seated randomly around a circular table. Then, the conditional probability that the Indian man is seated adjacent to his wife given that each American man is seated adjacent to his wife is
a. $\dfrac{1}{2}$
b. $\dfrac{1}{3}$
c. $\dfrac{2}{5}$
d. $\dfrac{1}{5}$

Answer 1

Hint : First of all we need to understand that in a circle there is no starting point as well as no ending point as compared to a row or queue, so we go for the number of arrangements as $\left( n-1 \right)!$ where $n$ is the number of seats or people. We are going to consider two cases and in both of them the Indian man is fixed on one seat and his wife is seated on the right of him in first case, after that in second case, she is seated on left of him. At the end we will use the conditional probability formula, $P\left( A/B \right)=\dfrac{P\left( A\cap B \right)}{P\left( B \right)}=\dfrac{n\left( A\cap B \right)}{n\left( B \right)}$, where $P\left( B \right)$ is probability that each American man sits with his wife and $P\left( A \right)$ is the probability that the Indian man sits next to his wife.

Complete step by step solution :
Now the question is divided in two parts, first we will use permutation and combination to find the total possible arrangements by following the conditions given in the question and the second part is that we will use the conditional probability formula to find the final answer of the question.
Now proceeding with the permutation and combination part of the question,
First we need to understand that why and how the number of arrangements changes when the number of positions are same but the manner in which positions are presented is different. For example we are going to compare the arrangement in a queue or row with the arrangement in a circle or rounded table.
Suppose we have $n$ people and we have a round table with $n$ seats arranged around the table in circular manner such that the seats are pointing towards the centre of the circular table, and we are comparing it with a row which has $n$ seats.
When we want to make first person sit in any one position in the row of $n$ seats then we have $n$ choices, similarly for second person to sit there are $\left( n-1 \right)$ choices and for third there are $\left( n-2 \right)$ choices it will go on until all the seats are filled with people and the last person will have only $1$ choice left at the end, so we will end up with answer as $n!$, as every position or seat is different and can be analyzed as such.
$n\times \left( n-1 \right)\times \left( n-2 \right)\times ............2\times 1=n!$ This is the answer.
Now when we want to make first person sit on the circular table in any one of the seats then we have $n$ choices but all seats are identical as there are no positions, and we cannot differ one position by another until there is some irregularity in the table, as there were in the row of $n$ seats.
Now if we recall that when we want to calculate the number of permutations or arrangements of $n$ objects out of which $p$ are alike and of one kind, similarly, $q$ are alike and of second kind then the answer will be $\dfrac{n!}{p!q!}$ we divide because there will be repetitions of some combinations so we will divide the total number of arrangements by the factorial of number of objects alike of one kind and when there are more than one kind of alike objects then further divide the answer by the factorial of number of objects of other kind and do same for every other kind.
Now coming back to our question we want to make first person sit on any one seat of round table then we must have $n$ different choices which look similar to the person we made sit in first chance, every seat will be same for the first person so it seems we have only $1$ choice because due to the above rule we have answer as $\dfrac{n!}{n!}$ which is $1$ because all the seats were identical to the person arriving first at the table.

From now on the question is same as arranging $\left( n-1 \right)$ people on $\left( n-1 \right)$ seats in a row because now the second person will encounter the first one sitting on the table and every seat will be distinguishable by the second person as the first person is acting similar as the origin in the Cartesian plane, a standard for measuring change.

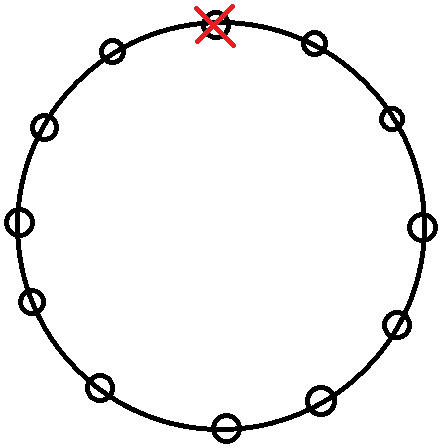
Now coming back to our original question we have fixed the Indian man seat and now we want to fix the seat of his wife but immediately adjacent to him and there are two choices one is left of him and the other is right of him but the number of arrangements in both cases will be same so it is logical to find the permutations in one case and then multiply it by $2$ but we also have to arrange the other couples together in order to find the actual number of arrangements of occurrence of both events A and B together which is $n\left( A\cap B \right)$, so the arrangements are like, one of the seats adjacent to the Indian man is vacant as the other is occupied by his wife so the number of choices are $10$ as there are $10$ people left but the next adjacent seat to this person will have only $5$ choices because the condition for couple must be satisfied so if one gender occupied the seat right next to Indian man then the other gender only can occupy the seat next to this person who is right next to the Indian man and both the gender are equal in number.

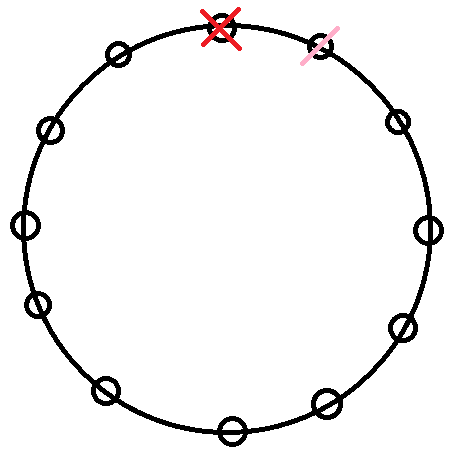
Now on third seat to the right of Indian man there can be only $8$ choices because $2$ seats were occupied earlier by $2$ people so $8$ people left and adjacent to this person there can be $4$ choices of person due to couple condition.
Now on the fifth to the right of the Indian man there can be $6$ choices because earlier $6$ seats are filled by $6$ people and the adjacent to this person can have only $3$ choices due to couple condition.
Now at the second position to the left of the Indian man we have $4$ choices left and the seat adjacent to this person can have only $2$ choices due to couple condition.
Now at the fourth position to the left of the Indian man can have only $2$ choices and the seat adjacent to this person can have only one position as only one person is left.
In the figure, the red cross represents the Indian man's position and the pink slashes represents his wife's positions and the choices are mentioned near the seats represented by small circles.

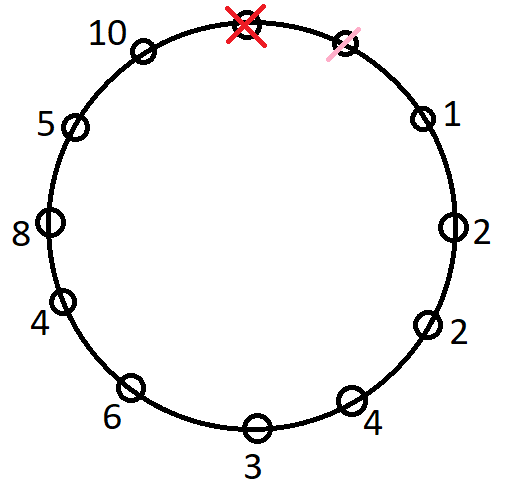
Now the final answer is $2\times \left( 10\times 5\times 8\times 4\times 6\times 3\times 4\times 2\times 2\times 1 \right)=921600$ which represents the value of $n\left( A\cap B \right)$ and now we want to find the value of number of combinations satisfying the event B which is $n\left( B \right)$. Now to find it we need to adapt the same ideology we did earlier but the difference here is that we need to change the position of the Indian man's wife because we need to consider all cases when American couples are seated together. Now we have found out the number of arrangements when all the couples are seated together but we have to find the ones in which the Indian couple is not seated together. The number of arrangements done earlier for American couples will be same it is just that the position of Indian man's wife will change and there are only $4$ positions where she can be seated because there should be even number of seats available between Indian man and his wife so that American couple condition is followed because a couple needs two seats adjacent to each other.

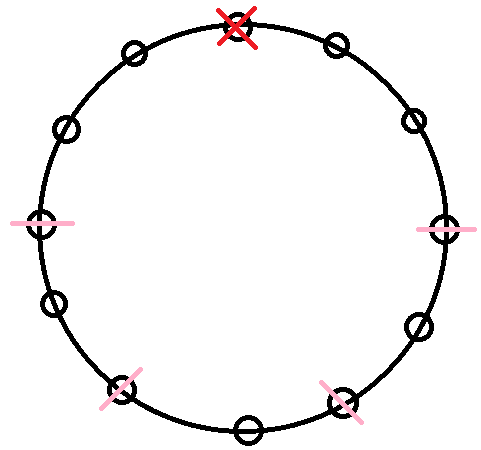
So now the number of arrangements for American couples to seat are $4\times \left( 10\times 5\times 8\times 4\times 6\times 3\times 4\times 2\times 2\times 1 \right)=1843200$ and now the conditional probability for Indian man to seat next to his wife when all American men are sitting next to their respective wives, is,
Conditional probability formula for occurrence of event A when event B has already occurred.
$P\left( A/B \right)=\dfrac{P\left( A\cap B \right)}{P\left( B \right)}=\dfrac{n\left( A\cap B \right)}{n\left( B \right)}$, where $P\left( B \right)$ is probability that each American man sits with his wife and $P\left( A \right)$ is the probability that the Indian man sits next to his wife, and $P\left( A\cap B \right)$ is the probability of occurrence of both events together at once.
Now by putting the known values in the formula, we get,
$P\left( A/B \right)=\dfrac{921600}{1843200}=\dfrac{9216}{18432}$
$P\left( A/B \right)=\dfrac{9216}{18432}=\dfrac{1}{2}$

Note : Now in these types of questions always approach the solution step by step frame the solution in your mind. Whenever dealing with rounded table questions always remember that for $n$ seats the number of arrangements will be $\dfrac{n!}{n}=\left( n-1 \right)!$ we divide by $n$ because there are $n$ different perceptions to watch the people sitting but there is only one perception we need to consider because by changing our perception their sitting arrangement is not changing actually, so we can also understand this concept in this way. We can also use the symbols ${}^{n}{{P}_{r}}$ and ${}^{n}{{C}_{r}}$ to evaluate this question and it is more easy and short method to perform in examination.