Solveeit Logo
Login

Question

Question: One end of uniform wire of length \[L\] and of weight \[W\] is attached rigidly to a point in the ro...

One end of uniform wire of length LL and of weight WW is attached rigidly to a point in the roof and a weight W1{W_1} is suspended from the lower end. If AA is the area of cross-section of the wire, the stress in the wire at a height 3L4\dfrac{{3L}}{4} from its lower end is:
A. W1A\dfrac{{{W_1}}}{A}
B. W1+W4A\dfrac{{{W_1} + \dfrac{W}{4}}}{A}
C. W1+3W4A\dfrac{{{W_1} + \dfrac{{3W}}{4}}}{A}
D. W1+WA\dfrac{{{W_1} + W}}{A}

Explanation

Solution

The formula for stress is given by,
Stress=ForceArea=FS{\text{Stress}} = \dfrac{{{\text{Force}}}}{{{\text{Area}}}} = \dfrac{F}{S}.
Weight per unit length
=WL= \dfrac{W}{L}

Complete step by step solution:
Weight: An object’s weight is the force of gravity on the item, which can be defined as the mass times the gravitational acceleration, w = mgw{\text{ }} = {\text{ }}mg. Provided that the weight is a force, the newton is its SI unit.
Let us consider the following diagram in order to solve the problem.

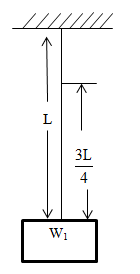
From the above diagram,
Weight per unit length
=WL= \dfrac{W}{L}
Therefore, the weight of 3L4\dfrac{{3L}}{4}th wire is given by,
3L4×WL=3W4\dfrac{{3L}}{4} \times \dfrac{W}{L} = \dfrac{{3W}}{4}

Again, in physics stress is the force that acts on a material's unit field. The tension effect on a body is known as pressure. The body may become deformed by stress.
The formula for stress is given by,
Stress=ForceArea=FS{\text{Stress}} = \dfrac{{{\text{Force}}}}{{{\text{Area}}}} = \dfrac{F}{S} …… (i)

A force is any movement that can alter an object's motion while unopposed. A force may cause an item to alter its velocity, i.e. to accelerate with time.
Now, Total force = Suspended weight + weight of wire.

Therefore,
F=W1+3W4F = {W_1} + \dfrac{{3W}}{4}
Now place the value of force, FF in equation (i).
i.e.
Stress =W1+3W4S = \dfrac{{{W_1} + \dfrac{{3W}}{4}}}{S}

Hence, option (C) is correct.

Note: Given, the weight per unit length =WL = \dfrac{W}{L}. Now obtain the value of the weight of 3L4\dfrac{{3L}}{4}th wire from the above form. Remember that total force is equal to the addition of the suspended weight along with the weight of the wire. Now place the value of force in the formula of stress, which is given by,
Stress=ForceArea=FS{\text{Stress}} = \dfrac{{{\text{Force}}}}{{{\text{Area}}}} = \dfrac{F}{S}. Hence, the final answer is obtained.