Question

One end of a stick with mass m and length l is pivoted on a wall and the other end rests on a frictionless floor, as shown in the figure. Let ${{F}_{L}}$ and${{F}_{R}}$ be the vertical forces on the left and the right ends of the sticks, respectively. Then:
a)${{F}_{L}}=mg/2$
b)${{F}_{L}}<{{F}_{R}}$
c)${{F}_{L}}={{F}_{R}}$
d)${{F}_{L}}=F=mg\cos \theta$

Answer 1

Firstly, draw the free body diagram of the stick to get the clear view of all the forces acting on the stick. Since the floor is frictionless, this means that the friction component of the force will be zero. And for equilibrium, the net sum of the forces on pivot should be zero. Resolve the forces into vertical and horizontal components and then equate the vertical and horizontal forces with their respective counterparts.

Complete step by step answer: The free body diagram of the stick is given below:

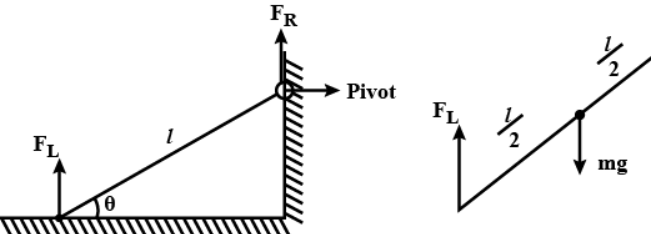
As we know that for the pivot to be in equilibrium the net sum of the forces should be zero.
So, for the pivot to be in equilibrium, we have:
$\sum{{{F}_{pivot}}=0}......(1)$
${{F}_{L}}\times 1\cos \theta =mg\times \dfrac{l}{2}\cos \theta$
${{F}_{L}}=\dfrac{mg}{2}......(2)$
Now, by resolving all the forces in the vertical direction, we get:
$\sum{{{F}_{vertical}}=0}$
${{F}_{L}}+{{F}_{R}}=mg$
From equation (2), we get:
${{F}_{R}}=\dfrac{mg}{2}$
Hence, ${{F}_{R}}={{F}_{L}}=\dfrac{mg}{2}$
Therefore, choice (a) is the answer.

Note: In order to answer this question, one must have knowledge of free body diagrams. A free body diagram (force diagram or FBD) is a graphical illustration used to visualize the applied forces, moments, and resulting reactions on a body in a given condition. They depict a body or connected bodies with all the applied forces and moments, and reactions, which act on the body. The body may consist of multiple internal members (such as a truss), or be a compact body (such as a beam). A series of free bodies and other diagrams may be necessary to solve complex problems.