Question
Question: One end of a spring of natural length h and spring constant K is fixed on the ground and the other i...
One end of a spring of natural length h and spring constant K is fixed on the ground and the other is fitted with a smooth ring of mass m which is allowed to slide on a horizontal rod fixed at a height h. Initially the spring makes an angle of 37∘ with the vertical when the system is released from rest. Find out the speed of the ring when the spring becomes vertical.
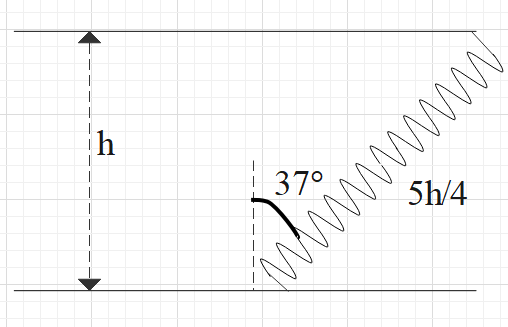
a) v=3hmk
b) v=4hm2k
c) v=4hmk
d) v=4h2mk
Solution
The initial length of the spring, when in equilibrium position is h. After the system is released from rest, let us assume that the spring is extended by x. So, the net length of spring is (h+x) which is given as: 45h. So, using this relation, find the value of x. Then apply, work energy theorem as: 21kx2=21mv2 where change in potential energy is equal to change in kinetic energy, to find the value of velocity.
Complete step by step answer:
As we have assumed that the extension in the system after it is released from the rest is x.
So, the final length can be given as:
(h+x)=45hx=45h−hx=4h......(1)
Now, apply work-energy theorem to the system, we get:
Change in potential energy = Change in kinetic energy
⇒21kx2=21mv2⇒21k(4h)2=21mv2⇒mk(4h)2=v2⇒v=4hmk
Hence, we get: v=4hmk.
So, the correct answer is “Option C”.
Note:
The work-energy theorem states that the net work done by the forces on an object equals the change in its kinetic energy, i.e. W=ΔKE
So, for the spring system, work done is W=21kx2
And we know that kinetic energy is given as: KE=21mv2
Hence, work energy theorem for a spring system is: 21kx2=21mv2.
