Question
Question: One end of a spring of force constant \(k\) is fixed to a vertical wall and another to a body of mas...
One end of a spring of force constant k is fixed to a vertical wall and another to a body of mass m resting on a smooth horizontal surface. There is another wall at the distance x0 from the body. The spring is then compressed by 3x0 and released.The time taken to strike the wall from the instant of release is ? (given sin−1(31)=(9π))
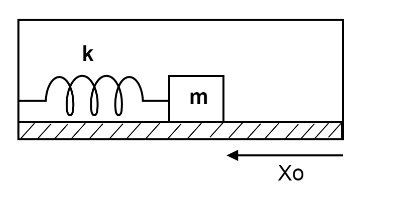
A. 6πkm
B. 32πkm
C. 4πkm
D. 911πkm
Solution
In this question, we have to calculate the time taken by the mass to strike from the instant of release. This can be achieved by using the concept of displacement of a body from mean position and time needed to cover the distance from compressed position to mean position.
Complete step by step answer:
The total amplitude of the motion is A=2x0. The time needed to cover from compressed position to mean position is 4T, where T is the total time required to do the motion.
Now, the displacement from the mean position to x0 , time taken t will be given as
y=Asinwt
⇒x0=2x0sinwt
But w=T2π, So,
⇒x0=2x0sinT2πt
solving for the value of t, we get t=12T−−−−−−(1)
Thus, Time taken to hit the wall is 12T+4T=3T−−−−−−(2)
Now, If mass m is suspended from the spring of force constant K , time period is given as
T=2πkm
So, Time taken to hit the wall is 3T=32πkm.
Hence, option B is correct.
Note: The particle performing SHM starting from mean position is given by x=asinwt. The period of SHM does not depend on amplitude or energy of the particle. When the spring is compressed by 3x0 , the total path of the particle is divided into four equal parts of time 4T.
