Question

One end of a spring is fixed to the ceiling and other end is attached to a block. The block is released when spring is relaxed. The product of time period and amplitude is 8 S.I. units. Spring is cut in two equal parts and the two parts are attached to the block as shown in figure. The block is released when both springs are relaxed. Now find the product of time period and amplitude in S.I. units.

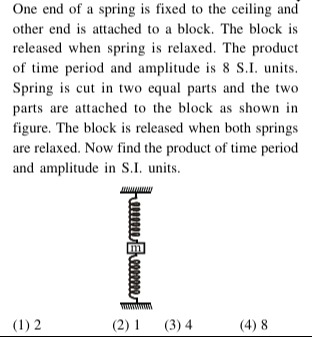
• A. 2
• B. 1
• C. 4
• D. 8

Answer 1

Answer: (D)

8

Answer 2

Let the original spring constant be $k$. The time period is $T_1 = 2\pi \sqrt{\frac{m}{k}}$ and the amplitude is $A_1 = \frac{mg}{k}$. We are given $T_1 \times A_1 = 8$. When the spring is cut into two equal parts, each part has a spring constant of $2k$. When attached in series, the effective spring constant $k_{eff}$ is given by $\frac{1}{k_{eff}} = \frac{1}{2k} + \frac{1}{2k} = \frac{1}{k}$, so $k_{eff} = k$. The new time period is $T_2 = 2\pi \sqrt{\frac{m}{k_{eff}}} = 2\pi \sqrt{\frac{m}{k}} = T_1$. The new amplitude is $A_2 = \frac{mg}{k_{eff}} = \frac{mg}{k} = A_1$. Therefore, $T_2 \times A_2 = T_1 \times A_1 = 8$.