Question

One end of a glass rod of refractive index is $n=1.5$ spherical surface of radius of curvature $R$ . The centre of the spherical surface lies inside the glass. A point object placed in air on the axis of the rod at the point $P$ has its real image inside glass at the point $Q$ (see figure). A line joining the points $P$ and $Q$ cuts the surface at $O$ such that $OP=20Q$ . The distance $PO$ is

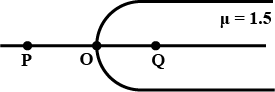
$(A)$ $8R$
$(B)$ $7R$
$(C)$ $2R$
$(D)$ None of these

Answer 1

Hint : We will be solving this question using the relation between refractive index of two medium and the distance between object and image from pole
For spherical surfaces
$\dfrac{{{\mu }_{2}}}{v}-\dfrac{{{\mu }_{1}}}{u}=\dfrac{{{\mu }_{2}}-{{\mu }_{1}}}{R}$
Where ${{\mu }_{2}}$ is refractive index of second medium (here glass)
${{\mu }_{1}}$ is refractive index of first medium (here air)
$v$ is distance of object from pole of spherical surface (here OP)
$u$ is distance of image from pole of spherical surface (here OQ)
$R$ is the radius of curvature of the spherical surface.

Complete Step By Step Answer:
Foe spherical surfaces above mentioned relation holds good
$\dfrac{{{\mu }_{2}}}{v}-\dfrac{{{\mu }_{1}}}{u}=\dfrac{{{\mu }_{2}}-{{\mu }_{1}}}{R}$
Where ${{\mu }_{2}}$ is refractive index of second medium (here glass)
${{\mu }_{1}}$ is refractive index of first medium (here air)
$v$ is distance of object from pole of spherical surface (here OP)
$u$ is distance of image from pole of spherical surface (here OQ)
$R$ is the radius of curvature of the spherical surface.
Here it is given that $OP=2OQ$ . By keeping sign convention in mind we get $OP=-2OQ$ (in magnitude, and in opposite sign). Given that the refractive index of glass is $1.5$ . Therefore, ${{\mu }_{2}}=1.5$ . We know that the refractive index of air is $1$ . Therefore, ${{\mu }_{1}}=1$ .
Now putting all known values in above equation, we get
$\dfrac{1.5}{OQ}-\dfrac{1}{OP}=\dfrac{1.5-1}{R}$
$\dfrac{1.5}{OQ}-\dfrac{1}{-2OQ}=\dfrac{0.5}{R}$
$\dfrac{1.5}{OQ}+\dfrac{1}{2OQ}=\dfrac{1}{2R}$
$\dfrac{1}{OQ}(1.5-0.5)=\dfrac{1}{2R}$
$\dfrac{1}{OQ}(2)=\dfrac{1}{2R}$
$4R=OQ$
$OP=2OQ=2(4R)$
$\Rightarrow OP=8R$
Hence, option $(A)$ is the correct answer.

Note :
Keep sign convention and value of refractive index in mind while solving such kinds of questions. Here if one did not keep the sign convention in distance of the object from the pole then the answer would be completely different and wrong and if the values of the refractive index were exchanged then one might get the wrong answer.