Question

One end of a copper rod of uniform cross-section and length 3.1 m is kept in contact with ice and the other end with water at ${{100}^{\circ }}C$. At what point along its length should a temperature of ${{200}^{\circ }}C$ be maintained so that in steady-state, the mass of ice melting be equal to that of the steam produced in the same interval of time? Assume that the whole system is insulated from the surrounding. Latent heat of fusion of ice and vaporization of water is 80 cal/gm and 540 cal/gm respectively
a) 40 cm from ${{100}^{\circ }}C$
b) 40 cm from ${{0}^{\circ }}C$
c) 125 cm from ${{100}^{\circ }}C$
d) 125 cm from ${{0}^{\circ }}C$

Answer 1

Let us assume that the point will lie at distance x m. Now, by using the formula $Q=\dfrac{KA}{l}\Delta T$ , find the rate of heat for both ice and water. Also, we know that: $Q=m\times s$, where m is mass and s is the specific heat of fusion for ice and specific heat of evaporation for water. So, get the value of specific heats in terms of x. Divide both the equations and substitute the value of latent heats and get the value of x.

Complete step by step answer:

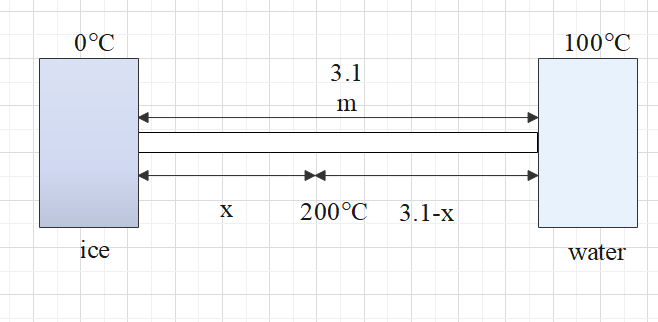
The heat rate by using the formula $Q=\dfrac{KA}{l}\Delta T=m\times s$
For ice:
${{Q}_{1}}=\dfrac{KA}{x}\left( 200-0 \right)=m\times {{s}_{ice}}......(1)$
For water:
${{Q}_{2}}=\dfrac{KA}{\left( 3.1-x \right)}\left( 200-100 \right)=m\times {{s}_{water}}......(2)$
Divide equation (1) by (2), we get:

& \dfrac{\dfrac{KA}{x}\left( 200-0 \right)}{\dfrac{KA}{\left( 3.1-x \right)}\left( 200-100 \right)}=\dfrac{m\times {{s}_{ice}}}{m\times {{s}_{water}}} \\\ & \dfrac{620-200x}{100x}=\dfrac{{{s}_{ice}}}{{{s}_{water}}}......(3) \\\ \end{aligned}$$ Since it is mentioned that Latent heat of fusion of ice and vaporisation of water are 80 cal/gm and 540 cal/gm respectively So, we can write equation (3) as: $\begin{aligned} & \dfrac{620-200x}{100 x}=\dfrac{80}{540} \\\ & \dfrac{31-10x}{5x}=\dfrac{4}{27} \\\ & 837-270x=20x \\\ & 290x=837 \\\ & x=2.88m \\\ \end{aligned}$ So, the length of point from steam chamber is $\begin{aligned} & \left( 3.1-x \right)=3.1-2.88 \\\ & =0.22m \\\ & =22cm \end{aligned}$ **So, the correct answer is “Option B”.** **Note:** Latent heat or specific heat is defined as the heat or energy that is absorbed or released during a phase change of a substance. It could either be from a gas to a liquid or liquid to solid and vice versa. Latent heat is related to a heat property called enthalpy.