Question

One diagonal of a square is the portion of the line $7x+5y=35$ intercepted between the axes. Determine the extremities of the other diagonal.

Answer 1

We have been given that the portion of the line $7x+5y=35$which is intercepted between the axes is one of the diagonals of a square. To find the extremities of the other diagonal, we will first find the coordinates of the given diagonal to find the midpoint and the length of the diagonal and then the slope of that diagonal. Using the slope of the given line, we will find the slope of the second diagonal as they are perpendicular to each other and hence the product of their slopes will be equal to -1. Then we will use the formula: if the slope of a line is given by $\tan \theta$ then the points $\left( x,y \right)$ at a distance ‘r’ from a fixed point $\left( h,k \right)$ on the line is given by $\left( x=h\pm r\cos \theta ,y=k\pm r\sin \theta \right)$ and hence we will find the required coordinates.

Complete step by step answer:
Now, we have been given that the portion of the line $7x+5y=35$which is intercepted between the axes is one of the diagonals of a square.
So, the coordinates of one diagonal of the square are the coordinates of the intercepts formed by the line $7x+5y=35$.

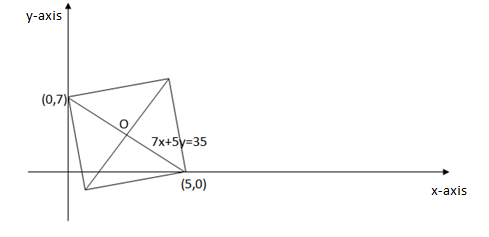
The coordinates of intercepts of a line $\dfrac{x}{a}+\dfrac{y}{b}=1$ are $\left( a,0 \right)$ and $\left( 0,b \right)$ where ‘a’ is the x-intercept and ‘b’ is the y-intercept.
Thus, transforming the equation of the given line in the form of $\dfrac{x}{a}+\dfrac{y}{b}=1$ , we will get:

& 7x+5y=35 \\\ & \Rightarrow \dfrac{7x}{35}+\dfrac{5y}{35}=1 \\\ & \Rightarrow \dfrac{x}{5}+\dfrac{y}{7}=1 \\\ \end{aligned}$$ From this, we can see that the coordinates of the given diagonal will be $\left( 5,0 \right)$ and $\left( 0,7 \right)$ . Now, we know that the diagonals of a square bisect each other perpendicularly. Thus, the mid-point O of the given diagonal will be both the point of intersection with the other diagonal and the midpoint of the other diagonal. Thus, we will find the point of the given diagonal. Now, we know that the midpoint $\left( x,y \right)$ of two points $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$ is given by the formula: $\begin{aligned} & x=\dfrac{{{x}_{1}}+{{x}_{2}}}{2} \\\ & y=\dfrac{{{y}_{1}}+{{y}_{2}}}{2} \\\ \end{aligned}$ Here, $\begin{aligned} & \left( {{x}_{1}},{{y}_{1}} \right)=\left( 5,0 \right) \\\ & \left( {{x}_{2}},{{y}_{2}} \right)=\left( 0,7 \right) \\\ \end{aligned}$ Thus, the point O $\left( x,y \right)$ is given by: $\begin{aligned} & x=\dfrac{5+0}{2} \\\ & y=\dfrac{0+7}{2} \\\ & \Rightarrow x=\dfrac{5}{2} \\\ & \Rightarrow y=\dfrac{7}{2} \\\ \end{aligned}$ Thus, the point O is $\left( \dfrac{5}{2},\dfrac{7}{2} \right)$ . Now, we will find the slope of the other diagonal. We have been given the equation of one diagonal as $$7x+5y=35$$. This equation can be written in the form of $y=mx+c$ where ‘m’ is the slope of the line and ‘c’ is the y-intercept. Transforming the equation of the given diagonal into slope-intercept form we get: $\begin{aligned} & 7x+5y=35 \\\ & \Rightarrow 5y=-7x+35 \\\ & \Rightarrow y=\dfrac{-7x}{5}+\dfrac{35}{5} \\\ & \Rightarrow y=\dfrac{-7}{5}x+7 \\\ \end{aligned}$ Thus, the slope of the given diagonal is $\dfrac{-7}{5}$ . Now, we know that the diagonals of a square bisect each other perpendicularly. Thus, the product of the slopes of the equations of the diagonals is equal to -1. Let the slope of the given diagonal be ${{m}_{1}}$ and the slope of the diagonal whose extremities have to be found be ${{m}_{2}}$ . Thus, ${{m}_{1}}{{m}_{2}}=-1$ Now, we have already found out that ${{m}_{1}}=-\dfrac{7}{5}$ Thus, $\begin{aligned} & \left( -\dfrac{7}{5} \right){{m}_{2}}=-1 \\\ & \Rightarrow {{m}_{2}}=\dfrac{5}{7} \\\ \end{aligned}$ Thus, the slope of the other diagonal is $\dfrac{5}{7}$ . Now, we will find the length of the diagonal (both the diagonals of a square are equal). The extremities of the diagonal are (5,0) and (0,7). We can find the length of diagonal by using the distance formula $\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}$ Thus, the length of the diagonal is given as: $\begin{aligned} & l=\sqrt{{{\left( 5-0 \right)}^{2}}+{{\left( 0-7 \right)}^{2}}} \\\ & \Rightarrow l=\sqrt{{{\left( 5 \right)}^{2}}+{{\left( -7 \right)}^{2}}} \\\ & \Rightarrow l=\sqrt{25+49} \\\ & \Rightarrow l=\sqrt{74} \\\ \end{aligned}$ Now, the length of the extremities of the diagonal from the point O is $\dfrac{l}{2}$ which is equal to $\dfrac{\sqrt{74}}{2}$ . Now, we know that if the slope of a line is given by $\tan \theta $ then the points $\left( x,y \right)$ at a distance ‘r’ from a fixed point $\left( h,k \right)$ on the line is given by: $\begin{aligned} & x=h\pm r\cos \theta \\\ & y=k\pm r\sin \theta \\\ \end{aligned}$ Coordinates in this form are known as ‘parametric coordinates’. Thus, we can find the extremities of the diagonal by taking the fixed point as point O and thus the value of ‘r’ will be $\dfrac{\sqrt{74}}{2}$ and the point $\left( h,k \right)$ will be $\left( \dfrac{5}{2},\dfrac{7}{2} \right)$ Now, the slope is $\dfrac{5}{7}$ . Thus, $\tan \theta =\dfrac{5}{7}$ From this, we can find the value of $\cos \theta $ and $\sin \theta $ $\begin{aligned} & \tan \theta =\dfrac{5}{7} \\\ & \Rightarrow \sin \theta =\dfrac{5}{\sqrt{{{5}^{2}}+{{7}^{2}}}} \\\ & \Rightarrow \sin \theta =\dfrac{5}{\sqrt{74}} \\\ & \Rightarrow \cos \theta =\dfrac{7}{\sqrt{{{5}^{2}}+{{7}^{2}}}} \\\ & \Rightarrow \cos \theta =\dfrac{7}{\sqrt{74}} \\\ \end{aligned}$ Now, let the extremities of the other diagonal be $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$ Thus, $\left( {{x}_{1}},{{y}_{1}} \right)$is given as: $\begin{aligned} & {{x}_{1}}=\dfrac{5}{2}+\left( \dfrac{\sqrt{74}}{2} \right)\left( \dfrac{7}{\sqrt{74}} \right) \\\ & \Rightarrow {{x}_{1}}=\dfrac{5}{2}+\dfrac{7}{2} \\\ & \Rightarrow {{x}_{1}}=\dfrac{12}{2} \\\ & \therefore {{x}_{1}}=6 \\\ \end{aligned}$ $\begin{aligned} & {{y}_{1}}=\dfrac{7}{2}+\left( \dfrac{\sqrt{74}}{2} \right)\left( \dfrac{5}{\sqrt{74}} \right) \\\ & \Rightarrow {{y}_{1}}=\dfrac{7}{2}+\dfrac{5}{2} \\\ & \Rightarrow {{y}_{1}}=\dfrac{12}{2} \\\ & \therefore {{y}_{1}}=6 \\\ \end{aligned}$ Thus, $\left( {{x}_{1}},{{y}_{1}} \right)=\left( 6,6 \right)$ Now, $\left( {{x}_{2}},{{y}_{2}} \right)$ is given as: $\begin{aligned} & {{x}_{2}}=\dfrac{5}{2}-\left( \dfrac{\sqrt{74}}{2} \right)\left( \dfrac{7}{2} \right) \\\ & \Rightarrow {{x}_{2}}=\dfrac{5}{2}-\dfrac{7}{2} \\\ & \Rightarrow {{x}_{2}}=\dfrac{-2}{2} \\\ & \therefore {{x}_{2}}=-1 \\\ & {{y}_{2}}=\dfrac{7}{2}-\left( \dfrac{\sqrt{74}}{2} \right)\left( \dfrac{5}{2} \right) \\\ & \Rightarrow {{y}_{2}}=\dfrac{7}{2}-\dfrac{5}{2} \\\ & \Rightarrow {{y}_{2}}=\dfrac{2}{2} \\\ & \therefore {{y}_{2}}=1 \\\ \end{aligned}$ Thus, $\left( {{x}_{2}},{{y}_{2}} \right)=\left( -1,1 \right)$ Thus, the extremities of the other diagonal are $\left( 6,6 \right)$ and $\left( -1,1 \right)$ **Note:** While using the parametric coordinates, be sure that there will be only two coordinates concluded from that formula, one by adding the given quantities and one by subtracting them. There can be no mix-matching, either only addition in both x and y coordinates or subtraction. The point obtained by the mix-match will not be valid.