Question

One diagonal of a square is the portion of the line $\sqrt{3}x+y=2\sqrt{3}$ intercepted by the axes, the extremity of the other diagonals is
a) $\left( 1+\sqrt{3} \right),\left( \sqrt{3}-1 \right)$
b) $\left( 1+\sqrt{3} \right),\left( \sqrt{3}+1 \right)$
c) $\left( 1-\sqrt{3} \right),\left( \sqrt{3}-1 \right)$
d) $\left( 1-\sqrt{3} \right),\left( \sqrt{3}+1 \right)$

Answer 1

We will write the equation of line the intercept form given by $\dfrac{x}{a}+\dfrac{y}{b}=1$ .We will get to know the x and y-intercepts of the line which will the extreme point of our one diagonal. We will calculate the slope of one diagonal using the equation of the line by writing it in the form $y=mx+c$, m will be the slope. We will calculate the slope of the other diagonal as we know that ${{m}_{1}}{{m}_{2}}=-1$. We will calculate the point where the diagonal intersects each other by using the Midpoint Formula. We will calculate the length of the diagonal using the distance formula. We know that diagonal of a square bisect each other at ${{90}^{\circ }}$ and are equal in length. We can calculate the extreme points of the other diagonal using $\dfrac{x-{{x}_{1}}}{\cos \theta }=\dfrac{y-{{y}_{1}}}{\sin \theta }=r$

Complete step-by-step solution:
__
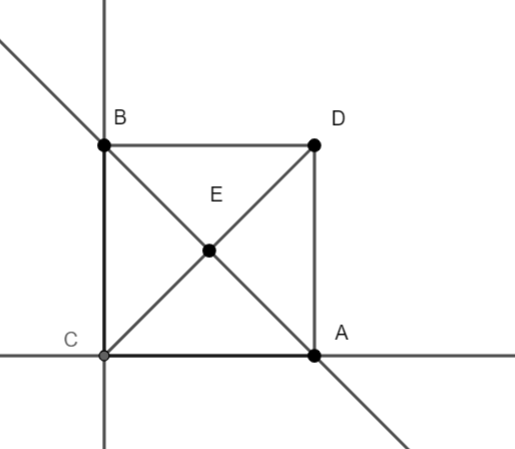
We have the above figure with us, we have a line cutting the axes at point A on x-axis and point B on y-axis. We can calculate the coordinates of A and B by converting the equation of line in intercept form given by $\dfrac{x}{a}+\dfrac{y}{b}=1$. Point A(a,0) and B(0, b).
$\Rightarrow \sqrt{3}x+y=2\sqrt{3}$
Above equation can be written as,
$\Rightarrow \dfrac{x}{2}+\dfrac{y}{2\sqrt{3}}=1$
From above equation e will get,
$\begin{aligned} & \Rightarrow A(2,0) \\\ & \Rightarrow B(0,2\sqrt{3}) \\\ \end{aligned}$
From equation $\sqrt{3}x+y=2\sqrt{3}$ we van see that slope of the diagonal is,
$\Rightarrow m=-\sqrt{3}$
We know that diagonals of square are perpendicular to each other, so, slope of other diagonal can be calculated using this relation ${{m}_{1}}{{m}_{2}}=-1$ ,we will get,
$\begin{aligned} & \Rightarrow -\sqrt{3}\times {{m}_{2}}=-1 \\\ & \Rightarrow {{m}_{2}}=\dfrac{1}{\sqrt{3}} \\\ \end{aligned}$
We can also write $\tan \theta =\dfrac{1}{\sqrt{3}}$ ,where $\theta$ is the angle of second diagonal from x-axis in positive direction.
Using $\tan \theta =\dfrac{1}{\sqrt{3}}$ we will get,
$\begin{aligned} & \Rightarrow \cos \theta =\dfrac{\sqrt{3}}{2} \\\ & \Rightarrow \sin \theta =\dfrac{1}{2} \\\ \end{aligned}$
We will calculate midpoint of diagonal point E using midpoint formula, we will get

& \Rightarrow x=\left( \dfrac{{{x}_{1}}+{{x}_{2}}}{2} \right) \\\ & \Rightarrow x=\dfrac{2+0}{2}=1 \\\ & \Rightarrow y=\left( \dfrac{{{y}_{1}}+{{y}_{2}}}{2} \right) \\\ & \Rightarrow y=\dfrac{0+2\sqrt{3}}{2}=\sqrt{3} \\\ \end{aligned}$$ We will get coordinates of $$\text{E}\left( 1,\sqrt{3} \right)$$ We will now calculate the length of the diagonal using distance formula, we will get, $$\begin{aligned} & \Rightarrow d\text{=}\sqrt{{{\left( {{x}_{1}}-{{x}_{2}} \right)}^{2}}+{{\left( {{y}_{1}}-{{y}_{2}} \right)}^{^{2}}}} \\\ & \Rightarrow d=\sqrt{{{\left( 2-0 \right)}^{2}}+{{\left( 0-2\sqrt{3} \right)}^{^{2}}}} \\\ & \Rightarrow d=\sqrt{16} \\\ & \Rightarrow d=4 \\\ \end{aligned}$$ The equation of diagonal which is perpendicular to a diagonal and passing through a given point can be calculated using $$\dfrac{x-{{x}_{1}}}{\cos \theta }=\dfrac{y-{{y}_{1}}}{\sin \theta }=\pm r$$, where $r=\dfrac{d}{2}$ as we know that the r is the radius of the circle and d is the diagonal of the circle so the radius is the half of diagonal, $$\Rightarrow \dfrac{x-1}{\dfrac{\sqrt{3}}{2}}=\dfrac{y-\sqrt{3}}{\dfrac{1}{2}}=\pm 2$$ We will first take, $$\dfrac{x-1}{\dfrac{\sqrt{3}}{2}}=\dfrac{y-\sqrt{3}}{\dfrac{1}{2}}=2$$, we will get, $$\begin{aligned} & \dfrac{x-1}{\dfrac{\sqrt{3}}{2}}=\dfrac{y-\sqrt{3}}{\dfrac{1}{2}}=2 \\\ & \\\ & \Rightarrow \dfrac{x-1}{\dfrac{\sqrt{3}}{2}}=2 \\\ & \\\ & \Rightarrow x=\sqrt{3}+1 \\\ & \\\ & \Rightarrow \dfrac{y-\sqrt{3}}{\dfrac{1}{2}}=2 \\\ & \\\ & \Rightarrow y=\sqrt{3}+1 \\\ & \\\ & \Rightarrow \left( x,y \right)=\left( \sqrt{3}+1,\sqrt{3}+1 \right) \\\ \end{aligned}$$ Now will take, $$\dfrac{x-1}{\dfrac{\sqrt{3}}{2}}=\dfrac{y-\sqrt{3}}{\dfrac{1}{2}}=-2$$, we will get, $$\begin{aligned} & \dfrac{x-1}{\dfrac{\sqrt{3}}{2}}=\dfrac{y-\sqrt{3}}{\dfrac{1}{2}}=-2 \\\ & \Rightarrow \dfrac{x-1}{\dfrac{\sqrt{3}}{2}}=-2 \\\ & \Rightarrow x=1-\sqrt{3} \\\ & \Rightarrow \dfrac{y-\sqrt{3}}{\dfrac{1}{2}}=-2 \\\ & \Rightarrow y=\sqrt{3}-1 \\\ \end{aligned}$$ $\Rightarrow \left( x,y \right)=\left( 1-\sqrt{3},\sqrt{3}+1 \right)$ **So the answer is b) $\left( 1+\sqrt{3} \right),\left( \sqrt{3}+1 \right)$** **Note:** Before attending this question, we must have a clear understanding of the properties of various geometric shapes, like in this question it is important to know that diagonals of square bisect and are perpendicular to each other. The student must know the various forms in which we can calculate the equation of the line. A clear understanding of the concepts of straight-line twice. Before marking the answer compare your answer and the option twice.