Question

On the side AB, BC, CA of a $\Delta ABC$ 3, 4, 5 distinct points (excluding vertices A, B, C) are respectively chosen. The number of triangles that can be constructed using these chosen points as vertices are,
A. 220
B. 215
C.210
D. 205

Answer 1

Hint: Draw $\Delta ABC$ and mark the number of distinct points on sides AB, BC, CA. Find the total number of triangles that can be formed by 3 , 4 and 5 points by using combination. Now find the total triangle that can be formed by $3+4+5=12$points. Subtract the no of triangles formed by 3,4,5 points from the total points to get the number of triangles that can be constructed.

Complete step-by-step answer:

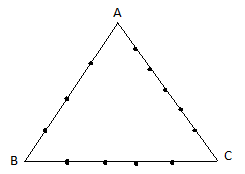
It is given that on side AB, BC, CA of a $\Delta ABC$, 3, 4, 5 distinct points are chosen. Consider the figure that is drawn. Side AB has 3 distinct points. Side BC has 4 distinct points and side AC has 5 distinct points.
Now adding all these points together, we will get 12 points which are used to form a triangle,
i.e. $3+4+5=12$ points.
We know that, to form a triangle, we need 3 points.
Therefore the total number of triangles that can be formed is given by the combination $^{12}{{C}_{3}}.$
$^{12}{{C}_{3}}$ is in the form of $^{n}{{C}_{r.}}$

& ^{n}{{C}_{r}}=\dfrac{n!}{(n-r)!r!} \\\ & ^{12}{{C}_{3}}=\dfrac{12!}{(12-3)!3!}=\dfrac{12!}{9!3!}=\dfrac{12\times 11\times 10\times 9!}{9!\times 3\times 2\times 1!}=\dfrac{12\times 11\times 10}{3\times 2}=220. \\\ \end{aligned}$$ [Cancelling like terms] $$\therefore $$Total number of triangles formed by 3 points $$=220$$. But this includes the number of triangles formed by 3 points on side AB. So it will be given by $$^{3}{{C}_{3}}=1.$$ $$^{3}{{C}_{3}}=\dfrac{3!}{(3-3)!3!}=\dfrac{3!}{0!3!}=1.$$ Thus the number of triangles formed by 4 points on BC$${{=}^{4}}{{C}_{3}}=4.$$ $$^{4}{{C}_{3}}=\dfrac{4!}{(4-3)!3!}=4.$$ The number of triangles formed by 5 points on CA $${{=}^{5}}{{C}_{3}}=10.$$ $$^{5}{{C}_{3}}=\dfrac{5!}{(5-3)!3!}=\dfrac{5!}{2!3!}=\dfrac{5\times 4\times 3!}{2\times 1\times 3!}=10.$$ Hence the required number of triangles = (Total number of triangles formed) – (Number of triangles formed by 3, 4, 5 points) $$\begin{aligned} & =220-(1+4+10) \\\ & =220-15 \\\ & =205. \\\ \end{aligned}$$ Hence the required number of triangles formed $$=205.$$ Option D is the correct answer. Note: There is no order for the number of triangles formed. So you can use the combination $$^{n}{{C}_{r}}$$ to find the number of triangles under each condition. We have taken here, r = 3 because to form a triangle, we need 3 points. Thus r = 3. Remember to find the total number of triangles formed by 12 points.