Question

On the same side of a tower, two objects are located. When observed from the top of the tower, their angles of depression are ${{45}^{\circ }}$ and ${{60}^{\circ }}$. If the height of the tower is 150 m, find the distance between the objects.

Answer 1

Hint:First of all we will suppose a tower of AB of length 150 m on the ground and C and D will be the two points on the same side of AB that represents two objects at finite distances from the tower AB. We know that angle of depression means the angle from the horizontal downward line or the line joining the object and observer’s eye. Now we will use trigonometric ratio to calculate the distance between the objects.

Complete step-by-step answer:
We have been given a tower of 150 m, two points located on the same side of the tower whose angle of depression are ${{45}^{\circ }}$ and ${{60}^{\circ }}$.
Let the tower be AB and the two points are C and D.

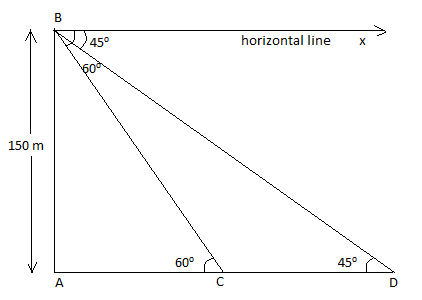
Since the horizontal line BX is parallel to AD.
$\Rightarrow \angle BCA=\angle CBX={{60}^{\circ }}$
Since these are alternate interior angles, when $BX||AD$ and BC cuts them.
Also, $\Rightarrow \angle BDA=\angle DBX={{45}^{\circ }}$
Since these are alternate interior angles, when $BX||AD$ and BD cuts them.
Now, in $\Delta ABC$ let us consider,
$\tan C=\dfrac{AB}{AC}$
Since tangent in any right angled triangle is the ratio of perpendicular to base.
$\Rightarrow \tan {{60}^{\circ }}=\dfrac{150}{AC}$
Since we have been given $\angle C={{60}^{\circ }}$ and AB = 150 m.
We know that $\tan {{60}^{\circ }}=\sqrt{3}$.
$\sqrt{3}=\dfrac{150}{AC}$
On cross multiplication, we get as follows:
$AC\sqrt{3}=150$
On dividing by $\sqrt{3}$we get as follows:

& \dfrac{AC\sqrt{3}}{\sqrt{3}}=\dfrac{150}{\sqrt{3}} \\\ & \Rightarrow AC=\dfrac{150}{\sqrt{3}} \\\ \end{aligned}$$ On rationalizing the irrational numbers, we get as follows: $$\begin{aligned} & \Rightarrow AC=\dfrac{150\times \sqrt{3}}{\sqrt{3}\times \sqrt{3}} \\\ & \Rightarrow AC=\dfrac{150\times \sqrt{3}}{\left( \sqrt{3} \right)2} \\\ & \Rightarrow AC=50\sqrt{3}m \\\ \end{aligned}$$ We know that the approximate value of $$\sqrt{3}=1.732$$. So by substituting the value we get as follows: $$\begin{aligned} & \Rightarrow AC=50\times 1.732 \\\ & \Rightarrow AC=86.60m \\\ \end{aligned}$$ Now in $$\Delta ABD$$, we have, $$\tan D=\dfrac{AB}{AD}$$ Since tangent in any right angled triangle is the ratio of perpendicular to base. $$\Rightarrow \tan {{45}^{\circ }}=\dfrac{100}{AD}$$ Since we have been given $$\angle D={{45}^{\circ }}$$ and AB = 100 m. We know that $$\tan {{45}^{\circ }}=1$$. $$\Rightarrow 1=\dfrac{150}{AD}$$ On cross multiplication, we get as follows: $$AD=150m$$ From the figure we get we can write, CD = AD – AC Since we have AD = 150 m and AC = 86.60 m $$\Rightarrow CD=\left( 150-86.60 \right)m=63.40m$$ Therefore, the distance between the two objects is equal to 63.40 m (approximately). Note: You must have to draw a diagram in these types of questions and then you can approach it according to the diagram. Also, be careful while calculating the value of AC and don’t use $$\tan {{60}^{\circ }}=\dfrac{1}{\sqrt{3}}$$ by mistake. Sometimes we get confused about the value of $$\tan {{60}^{\circ }}$$ which is $$\sqrt{3}$$ which is wrong.So take care of it while calculating.Students should remember the important trigonometric ratios and standard angles to solve these types of questions.