Question

On the interval $\left( {0,\dfrac{\pi }{2}} \right)$, the function $\log \sin x$is
1. Increasing
2. Decreasing
3. Neither increasing nor decreasing
4. None of the above

Answer 1

The given function is $\log \sin x$ and the given interval is $\left( {0,\dfrac{\pi }{2}} \right)$ . The $\sin$ function is increasing over the period $\left( {0,2\pi } \right)$during the intervals $\left( {0,\dfrac{\pi }{2}} \right)and\left( {3\dfrac{\pi }{2},2\pi } \right)$. We will first differentiate the given function and then find out whether the answer is an increasing or a decreasing function.
Formulae used in the problem are:
\eqalign{ & \dfrac{d}{{dx}}\left( {\log x} \right) = \left( {\dfrac{1}{x}} \right) \cr & \dfrac{d}{{dx}}\left( {\sin x} \right) = \cos x \cr & \dfrac{{\cos x}}{{\sin x}} = \cot x \cr}

Complete step-by-step solution:
The given function is $\log \sin x$
Let $f\left( x \right) = \log \sin x$
The derivative of $f\left( x \right)$ will be $f'\left( x \right)$
Therefore, differentiating on both sides, we get
$f'\left( x \right) = \left( {\dfrac{1}{{\sin x}}} \right) \times \left( {\cos x} \right)$
Further simplifying,
\eqalign{ & \Rightarrow f'(x) = \dfrac{{\cos x}}{{\sin x}} \cr & \Rightarrow f'(x) = \cot x \cr}
The given interval is $\left( {0,\dfrac{\pi }{2}} \right)$
In $\left( {0,\dfrac{\pi }{2}} \right)$, the $\cot$ function is positive. Hereby, making the function an increasing function.
Hence option (1) is the correct answer.
Additional Information:

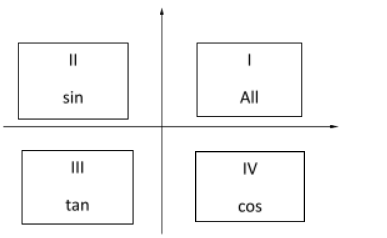
The above given graph tells us what functions are positive during what intervals starting from $0to\pi$. The quadrants are placed anticlockwise. We can remember this as ASTC rule.

Note: The $\log$ function has a derivative of $\dfrac{1}{x}$. Therefore, whatever is there in the place of x will go to the denominator. Remember the ASTC rule for all the functions. If the value falls in a quadrant where its positive, the function will be increasing, else it will be a decreasing function.