Question

On the basis of kinetic theory of kinetic theory of gases, derive an expression for the pressure exerted by gas.

Answer 1

We will start the solution by considering the gas in a closed cube of length l units and focus on only one particle in it. After that we will find its velocity and force exerted on it by any of the faces of the cube. By using the formula of root mean square velocity and pressure we will get the required value of the pressure.

Formula used:
${{f}^{2}}={{u}^{2}}+{{v}^{2}}+{{w}^{2}}$,
$P=mv$ where P is momentum, m is mass and v is velocity of the particle,
$\Delta P={{P}_{2}}-{{P}_{1}}$,
$\text{Time=}\dfrac{\text{Distance}}{\text{Speed}}$,
$\text{Force=}\dfrac{\text{mass }\\!\\!\times\\!\\!\text{ velocit}{{\text{y}}^{\text{2}}}}{\text{Total Distance Covered}}$,
$F=\dfrac{m{{v}_{1}}^{2}}{l}+\dfrac{m{{v}_{2}}^{2}}{l}+..+\dfrac{m{{v}_{n}}^{2}}{l}$,
$\text{pressure=}\dfrac{\text{Force}}{\text{Area}}$,
${{v}_{average}}=\sqrt{\dfrac{{{v}_{1}}^{2}+{{v}_{2}}^{2}+...+{{v}_{n}}^{2}}{n}}$
$J=mn$,
$\rho =\dfrac{J}{V}$ where J is total mass and V is total volume, $\rho$ is density of gas.

Complete answer:
We will take a cubic vessel with the length of I units with the consideration of the sides to be elastic. This results into the area of the cube as ${{l}^{2}}$ and the volume as ${{l}^{3}}$.
We will consider the following diagram for this question.

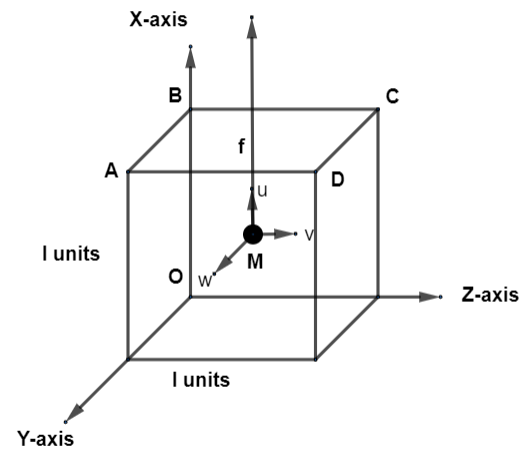
Consider the gas inside this vessel as 1 gram of molecules. Let all these molecules inside the gas are total in number as n with mass m each. Thus, the total mass of gas is $J=mn$. We will take one molecule M of mass m such that it travels with a velocity f and mark three components u, v, and w of it in x, y and z directions. This velocity f is taken out as ${{f}^{2}}={{u}^{2}}+{{v}^{2}}+{{w}^{2}}$….(i). Also, by momentum formula $P=mv$ where P is momentum, m is mass and v is velocity of the particle. So, we will have momentum of the first molecule as ${{P}_{1}}=m{{v}_{1}}$. Since, every particle of the gas is moving freely so, they will collide with faces of ABCD. This means that momentum changes after collision to ${{P}_{2}}=-m{{v}_{1}}$. So, by formula of change in momentum, we have

$\begin{aligned} & \Delta P={{P}_{2}}-{{P}_{1}} \\\ & \Rightarrow \Delta P=-m{{v}_{1}}-m{{v}_{1}} \\\ & \Rightarrow \Delta P=-2m{{v}_{1}} \\\ \end{aligned}$

As the length of the cube is l units so, It will cover a total distance of 2l and then collides ABCD. By the formula $\text{Time=}\dfrac{\text{Distance}}{\text{Speed}}$ we will get value of time travelled by the particle by $\text{Time=}\dfrac{2l}{{{v}_{1}}}$. This results in the number of collisions by the same particle as $\dfrac{{{v}_{1}}}{2l}$.

Thus, change in the momentum of the same molecule will be $-2m{{v}_{1}}\times \dfrac{{{v}_{1}}}{2l}=-\dfrac{m{{v}_{1}}^{2}}{l}$. By Newton's second law, the force applied to any object results in greater acceleration. Also, it results in the rate of change in momentum as equal to force applied on it. Thus, force applied on a molecule is $-\dfrac{m{{v}_{1}}^{2}}{l}$. Now, by Newton’s third law of motion, it explains action implying equal and opposite reactions. So, Force exerted on the same particle by the face ABCD is $\dfrac{m{{v}_{1}}^{2}}{l}$.

This force will be exerted on each and every molecule of the gas present inside the cube. Therefore, total force exerted on all particles of gas in x direction will be

$\begin{aligned} & F=\dfrac{m{{v}_{1}}^{2}}{l}+\dfrac{m{{v}_{2}}^{2}}{l}+..+\dfrac{m{{v}_{n}}^{2}}{l} \\\ & \Rightarrow F=\dfrac{m}{l}\left( {{v}_{1}}^{2}+{{v}_{2}}^{2}+..+{{v}_{n}}^{2} \right) \\\ \end{aligned}$

Now, we will use formula of pressure,

$\begin{aligned} & \text{pressure=}\dfrac{\text{Force}}{\text{Area}} \\\ & \Rightarrow \text{pressure=}\dfrac{F}{{{l}^{2}}} \\\ \end{aligned}$

This gives value of pressure exerted on the face ABCD as

$\begin{aligned} & \text{pressure=}\dfrac{F}{{{l}^{2}}} \\\ & \Rightarrow \text{pressure=}\dfrac{\dfrac{m}{l}\left( {{v}_{1}}^{2}+{{v}_{2}}^{2}+..+{{v}_{n}}^{2} \right)}{{{l}^{2}}} \\\ & \Rightarrow \text{pressure=}\dfrac{m}{{{l}^{3}}}\left( {{v}_{1}}^{2}+{{v}_{2}}^{2}+..+{{v}_{n}}^{2} \right) \\\ \end{aligned}$

Clearly, all faces of the cube are of the same length and area so, each face will exert the same pressure as that of ABCD. So, by using root mean square velocity, which means the square root of values of sum of velocity to the square by its number we get, the value of average square velocity of all particles. Thus, we get ${{v}_{average}}=\sqrt{\dfrac{{{v}_{1}}^{2}+{{v}_{2}}^{2}+...+{{v}_{n}}^{2}}{n}}$. By squaring both sides we get,

$\begin{aligned} & {{\left( {{v}_{average}} \right)}^{2}}=\dfrac{{{v}_{1}}^{2}+{{v}_{2}}^{2}+...+{{v}_{n}}^{2}}{n} \\\ & \Rightarrow n{{\left( {{v}_{average}} \right)}^{2}}={{v}_{1}}^{2}+{{v}_{2}}^{2}+...+{{v}_{n}}^{2} \\\ \end{aligned}$

So, the pressure will be $\text{pressure=}\dfrac{m}{{{l}^{3}}}n{{\left( {{v}_{average}} \right)}^{2}}$. Since, the volume V of the gas inside the cube is ${{l}^{3}}$ so, the formula gets reduced to $\text{pressure=}\dfrac{m}{V}n{{\left( {{v}_{average}} \right)}^{2}}$. As total mass is $J=mn$ so, $\text{pressure=}\dfrac{J}{V}{{\left( {{v}_{average}} \right)}^{2}}$.
By the formula of density of a gas which is $\rho =\dfrac{J}{V}$ therefore, $\text{pressure=}\rho {{\left( {{v}_{average}} \right)}^{2}}$.
Hence, the required value of pressure exerted by the gas inside the cube is $\text{pressure=}\rho {{\left( {{v}_{average}} \right)}^{2}}$.

Note:
The following points should be on fingertips to solve this question.
(1) All the particles of gas inside the cube will have momentums in the same way.
(2) The formula for momentum $P=mv$.
(3) We can start the solution by considering any face of the cube.
(4) If we $n=\dfrac{1}{3}N$ then, the formula of pressure will be $\text{pressure=}\dfrac{1}{3}\rho {{\left( {{v}_{average}} \right)}^{2}}$.