Question

On the axis of any parabola ${{y}^{2}}=4ax$there is a certain point K on the x-axis which has the property that, if a chord PQ of the parabola be drawn through it, then $\dfrac{1}{{{(PK)}^{2}}}+\dfrac{1}{{{(QK)}^{2}}}$ is same for all position of chord. Find the coordinate of K.
A.(4a,0)
B.(2a,0)
C.(a,0)
D.None of these

Answer 1

Hint : First we will draw a parabola whose vertex is on origin and opens on the right side. Then draw a cord which intersects the x-axis at a point K (0, d) (assume it). Now we will have a line PQ, Find the coordinate of P and Q and try to find the coordinate of K.

Complete step-by-step answer :
Draw the given parabola ${{y}^{2}}=4ax$ and also draw a chord PQ which is passing through point K having an angle $\theta$ with x axis which is basically line’s slope.

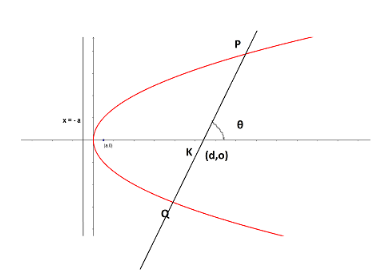
Equation of line PQ which is passing through K and having slope $\theta$ and equal distance from both axis ‘r’.
$\dfrac{x-d}{\cos \theta }=\dfrac{y-0}{\sin \theta }=r$
Now we can find the coordinates of P and Q.
$\begin{aligned} & P=[PK\cos \theta +d,PK\sin \theta ], \\\ & Q=[-QK\cos \theta +d,-QK\sin \theta ] \\\ \end{aligned}$ $(given:PK=QK=r)$
P and Q lies on parabola so it must satisfy the equation of parabola.
$\begin{aligned} & {{(PK)}^{2}}{{\sin }^{2}}\theta =4a(PK\cos \theta +d) \\\ & {{(PK)}^{2}}{{\sin }^{2}}\theta -PK.4a\cos \theta -4ad \\\ \end{aligned}$
……………….. (1)
$\begin{aligned} & {{(QK)}^{2}}{{\sin }^{2}}\theta =4a(-QK\cos \theta +d) \\\ & {{(QK)}^{2}}{{\sin }^{2}}\theta +QK.4a\cos \theta -4ad=0 \\\ \end{aligned}$
………………. (2)

Equation 1 and equation 2 is an quadratic equation,
$PK=\dfrac{4a\cos \theta +\sqrt{16{{a}^{2}}{{\cos }^{2}}\theta +16ad{{\sin }^{2}}\theta }}{2{{\sin }^{2}}\theta }$
We will ignore the negative value.
$QK=\dfrac{-4a\cos \theta +\sqrt{16{{a}^{2}}{{\cos }^{2}}\theta +16ad{{\sin }^{2}}\theta }}{2{{\sin }^{2}}\theta }$
We will ignore the negative value.
Now, we will have,
$\dfrac{1}{{{(PK)}^{2}}}+\dfrac{1}{{{(QK)}^{2}}}=\dfrac{2a{{\cos }^{2}}\theta +d{{\sin }^{2}}\theta }{2a{{d}^{2}}}$
It is given that the value of $\dfrac{1}{{{(PK)}^{2}}}+\dfrac{1}{{{(QK)}^{2}}}$ is same.
It should be independent from $\theta$ . To make it independent from $\theta$ , substitute $d=2a$ .
$\dfrac{1}{{{(PK)}^{2}}}+\dfrac{1}{{{(QK)}^{2}}}=\dfrac{2a{{\cos }^{2}}\theta +2a{{\sin }^{2}}\theta }{2a{{(2a)}^{2}}}=\dfrac{1}{4{{a}^{2}}}$
Hence the coordinate of K is (2a,0).
Option (B) is correct.

Note : Recall the equation of lines which two coordinate or one point and slope etc. are given. The parabola is defined as the locus of a point which moves so that it is always the same distance from a fixed point (called the focus) and a given line (called the directrix).