Question

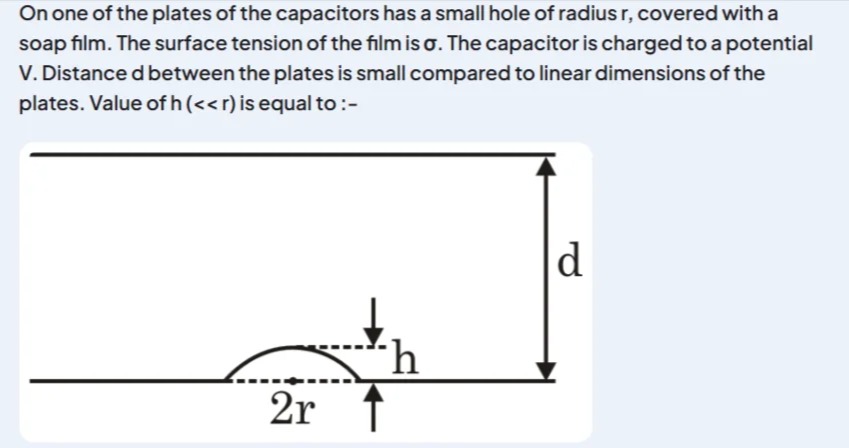
On one of the plates of the capacitors has a small hole of radius r, covered with a soap film. The surface tension of the film is $\sigma$. The capacitor is charged to a potential V. Distance d between the plates is small compared to linear dimensions of the plates. Value of h ($<<$ r) is equal to :-

Answer 1

h = $\frac{\epsilon_0 V^2 r^2}{16 \sigma d^2}$

Answer 2

The soap film bulges due to electrostatic pressure and is resisted by surface tension. The electrostatic pressure ($P_e$) is given by $P_e = \frac{1}{2} \epsilon_0 E^2$. With $E = V/d$, this becomes $P_e = \frac{\epsilon_0 V^2}{2d^2}$. The pressure due to surface tension ($\Delta P_{surface}$) for a bulge height $h \ll r$ is approximately $\frac{8\sigma h}{r^2}$. At equilibrium, $P_e = \Delta P_{surface}$, so $\frac{\epsilon_0 V^2}{2d^2} = \frac{8\sigma h}{r^2}$. Solving for $h$ yields $h = \frac{\epsilon_0 V^2 r^2}{16 \sigma d^2}$.