Question

On loading, a spring with bob, its period of oscillation in a vertical plane is T. If this spring pendulum is tied with one end to its frictionless table and made to oscillate in a horizontal plane, its period of oscillation will be –
A) T
B) 2T
C) $\dfrac{T}{2}$
D) Will not execute S.H.M

Answer 1

We need to understand the similarities and the differences between the oscillations made by a system of spring and pendulum in horizontal oscillations and in vertical oscillations. We can easily solve this problem with the idea of these.

Complete step-by-step solution
We are given a system of spring and bob which initially was hung from a roof and underwent an oscillation with a time period of ‘T’. We can see the figurative representation below.

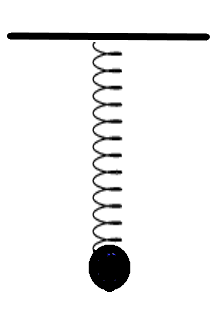
It is given that the spring-bob system undergoes an oscillation with time period T. We know that for a spring system, the angular frequency of oscillation is given as –
$\omega =\sqrt{\dfrac{k}{m}}$
Where k is the spring constant and m is the mass of the system.
We know that the time period related with this angular frequency as –

& T=\dfrac{2\pi }{\omega } \\\ & \therefore T=2\pi \sqrt{\dfrac{m}{k}} \\\ \end{aligned}$$ So, we get the time period of oscillation of the spring-bob system in the vertical plane as given above. Now, let us consider the same system of spring and bob in a horizontal plane. It is given that the table on which the system rests is frictionless. So, the oscillation will be dependent on the mass of the system and the spring constant as the first case. We can understand the oscillation from the below figure.  Now, we know that the time period for the oscillation is given as – $$T=\dfrac{2\pi }{\omega }$$ We can understand from the situation that the angular velocity of the system is same as the first one. So, the time period will be – $$\begin{aligned} & \omega =\sqrt{\dfrac{k}{m}} \\\ &\Rightarrow T=\dfrac{2\pi }{\omega } \\\ & \therefore T=2\pi \sqrt{\dfrac{m}{k}} \\\ \end{aligned}$$ So, we get that the time period for both the oscillations along the horizontal plane and the vertical plane remains the same. The time period is independent of the plane of oscillation. **The correct answer is option A.** **Note:** The time period in both the cases in our problem is the same. This is because the table on which the horizontal oscillation takes place is frictionless. This is not so in practical cases. As a result, the horizontal oscillation will not be an S.H.M, but a damped oscillation.