Question

On interchanging the resistances, the balance point of a meter bridge shifts to the left by $10cm$ . The resistance of their series combination is $1k\Omega$ . How much was the resistance on the left slot before interchanging the resistances?
A) $550\Omega$
B) $910\Omega$
C) $990\Omega$
D) $505\Omega$

Answer 1

To solve this question we have to use the concept of Wheatstone Meter Bridge. Under balanced conditions the galvanometer gives a zero reading i.e., the resistance gradient on the left side of the galvanometer and the right side of the galvanometer is equal. By using this we can easily find the value of the unknown resistance.

Formula Used:
$\dfrac{{{R_1}}}{l} = \dfrac{{{R_2}}}{{\left( {100 - l} \right)}}$
Here ${R_1}$ is the resistance on the left side of the galvanometer, ${R_2}$ is the resistance of the galvanometer, $l$ is the distance of the galvanometer from the left end and $100 - l$ is the distance of the galvanometer from the right end.

Complete step by step answer:
In the question the total resistance is given as $1k\Omega$i.e. $1000\Omega$. So,
$\Rightarrow {R_1} + {R_2} = 1000$
$\Rightarrow {R_2} = 1000 - {R_1}$
Here ${R_1}$ is the resistance on the left side of the galvanometer and ${R_2}$ is the resistance of the galvanometer in the initial condition.
The given question can be better understood using a figure.

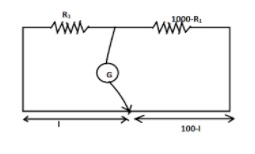
This is the initial condition of the Wheatstone bridge as given in the question. As it is in balance condition, we can use the formula of equal gradients on both sides.
$\Rightarrow \dfrac{{{R_1}}}{l} = \dfrac{{1000 - {R_1}}}{{\left( {100 - l} \right)}}$
Let this be equation 1.
It’s given that if we interchange the resistance on the right and resistance on the left, the balancing point shifts $10cm$to the left.
${l_{new}} = l - 10$ and
${l_{new}} - 100 = l + 10 - 100$
Here ${l_{new}}$ is the distance of the galvanometer from the left end for the new position and ${l_{new}} - 100$ is the distance of the galvanometer from the right end for the new position.

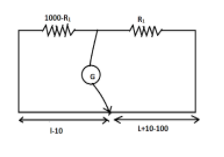
As this condition is also a balanced condition, we can use the formulae of balanced Wheatstone bridge. So,
$\Rightarrow \dfrac{{1000 - {R_1}}}{{{l_{new}}}} = \dfrac{{{R_1}}}{{\left( {100 - {\operatorname{l} _{new}}} \right)}}$
$\Rightarrow \dfrac{{1000 - {R_1}}}{{l - 10}} = \dfrac{{{R_1}}}{{\left( {100 - \left( {l + 10} \right)} \right)}}$
Let this be equation 2.
By solving equation 1 and 2 we will get the value of $l = 55cm$
By using this value of $l$in equation 1 we will get the value of ${R_1} = 550\Omega$.

Hence, option (A) is the right option.

Note: While solving the question related to Wheatstone bridge, it is very important to see if the Wheatstone bridge is in balanced condition or not. Also we have to be careful while selecting the sides of the resistance. Wrong selection of sides can lead to incorrect length calculations as well as incorrect resistance calculations.