Question

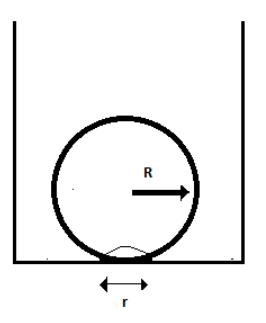
On heating water, bubbles being formed at the bottom of the vessel detach and rise. Take the bubbles to the spheres of radius $R$ and make a circular contact of radius $r$ with the bottom of the vessel. If $r << R$ and the surface tension of water is $T$, value of $r$ just before bubbles detach is: (density of water is $\rho$ )

$A.{{R}^{2}}\sqrt{\dfrac{2\rho g}{3T}}$
$B.{{R}^{2}}\sqrt{\dfrac{\rho g}{6T}}$
$C.{{R}^{2}}\sqrt{\dfrac{\rho g}{T}}$
$D.{{R}^{2}}\sqrt{\dfrac{3\rho g}{T}}$

Answer 1

We have to apply the concept of up-thrust. We have to use the fact that during detachment the excess pressure on the bubble will be equal to the up-thrust offered. Up-thrust is equal to the weight of the object displaced by the object. Excess pressure is defined as the difference between the atmospheric pressure and the internal pressure.
Formula used: We are using the following formula to solve this particular problem:-
$\dfrac{2T}{R}\pi {{r}^{2}}=\dfrac{4}{3}\pi {{R}^{3}}\rho g$.

Complete step by step solution:
From the problem given above we have following parameters with us:
Radius of the sphere is $R$ .
Circular contact of radius $r$
Surface tension is $T$
Density of water is $\rho$ .
We have the following figure with us:-

We know that during detachment of bubble force due to extra pressure is equal to the up-thrust offered.
Excess pressure is given as $\dfrac{2T}{R}$and therefore, force due to excess pressure is given as$\dfrac{2T}{R}\times \pi {{r}^{2}}$because force can be represented as the product of pressure and area.
Up-thrust is given with the relation $\dfrac{4}{3}\pi {{R}^{3}}\rho g$.
Force due to excess pressure is equal to up-thrust.
Mathematically we can write,
$\dfrac{2T}{R}\pi {{r}^{2}}=\dfrac{4}{3}\pi {{R}^{3}}\rho g$………….. $(i)$
Solving $(i)$ further we get
$\dfrac{T}{R}{{r}^{2}}=\dfrac{2}{3}{{R}^{3}}\rho g$
$\Rightarrow {{r}^{2}}=\dfrac{2}{3T}{{R}^{4}}\rho g$
$\Rightarrow r=\sqrt{\dfrac{2{{R}^{4}}\rho g}{3T}}$
Hence, $r={{R}^{2}}\sqrt{\dfrac{2\rho g}{3T}}$

Therefore, we get the correct answer and option $(A)$ is the correct.

Note:
In solving these types of problems we should consider the state of equilibrium of forces. Concept of up-thrust should be applied without any error in formula. We should remember the fundamental fact that force can be represented as the product of pressure and area. If we consider these things then our solution will also be correct most of the time.