Question

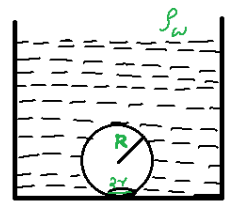
On heating water, bubbles being formed at the bottom of the vessel detach and rise. Take the bubbles to be spheres of radius R and make circular contact of radius r with the bottom of the vessel. If r < < R, the surface tension of water is T. Value of r just before the bubble detach is, (${{\rho }_{w}}$ is the density of water)

Answer 1

Hint: The water bubble at the bottom of the vessel experiences mainly two forces. One is the force due to buoyancy and the other one is the force due to surface tension of the water bubble with the vessel.

Complete step by step answer:
So we are given a vessel and in it, there is a bubble of radius R. The bubble is attached to the bottom of the vessel and the circular contact has a radius r. So when the bubble is about to detach from the bottom of the vessel the buoyancy will equal or greater than the surface tension of the bubble.
So the buoyant force acting on the bubble is given by,
${{\text{F}}_{\text{b}}}={{\text{ }\\!\\!\rho\\!\\!\text{ }}_{\text{w}}}\text{Vg}$…equation (1)
Where,
${{\text{ }\\!\\!\rho\\!\\!\text{ }}_{\text{w}}}$ is the density of water.
V is the volume of the bubble.
g is the acceleration due to gravity.
The force due to surface tension is given,
${{\text{F}}_{\text{s}}}=\text{Tl}$…… equation (2)

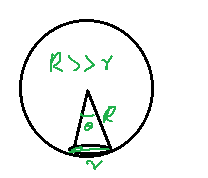
Where, T is the surface tension
l is the length of the bubble in contact, which is given by $\text{l}=\left( 2\pi r \right)\sin \theta$.
So the bubble is about to detach when these forces are equal.
${{\text{F}}_{\text{b}}}={{\text{F}}_{\text{s}}}$
From equation (1) and (2), we can write,
${{\text{ }\\!\\!\rho\\!\\!\text{ }}_{\text{w}}}\text{Vg}=\text{Tl}$
Substituting $V=\dfrac{4}{3}\pi {{R}^{3}}$ and $\sin \theta =\dfrac{r}{R}$, in the above equation, we get
${{\text{ }\\!\\!\rho\\!\\!\text{ }}_{\text{w}}}\left( \dfrac{4}{3}\pi {{R}^{3}} \right)\text{g}=\text{T}\left( \dfrac{r}{R}\left( 2\pi r \right) \right)$
$\therefore \text{ r}={{R}^{2}}\sqrt{\dfrac{2{{\rho }_{w}}g}{3T}}$
So the value of r at the time when the bubble is just about to detach from the bottom is given by $\text{ r}={{R}^{2}}\sqrt{\dfrac{2{{\rho }_{w}}g}{3T}}$

Note: Surface tension is the tendency of liquid surfaces to shrink into the minimum surface area possible. Surface tension is measured in force per unit length. Its SI unit is a newton per meter but the C.G.S unit of dyne per centimetre is also used.
Buoyancy or upthrust is an upward force exerted by a fluid that opposes the weight of a partially or fully immersed object.