Solveeit Logo
Login

Question

Question: On an open ground a motorist follows a track that turns to his left by an angle of \({60^ \circ }\) ...

On an open ground a motorist follows a track that turns to his left by an angle of 60∘{60^ \circ } after every 500 m. Starting from a given turn, specify the displacement of the motorist at the third, sixth and eighth turn. Compare the magnitude of the displacement with the total path length covered by the motorist in each case.

Explanation

Solution

Distance covered or total path covered is the total movement of an object without any regard to a specific direction. In physics, displacement is defined as the change in position of an object or how far an object is displaced from its initial position. It is a vector quantity

Formula Used:
D=d1+d2D = {d_1} + {d_2}
Where DD is the total distance and d1{d_1}, d2{d_2} are the paths taken.

Complete step by step solution:
From the given question we see that the path followed by the motorist is a regular hexagon with sides 500m. Let us draw a rough diagram for a better understanding of the question,

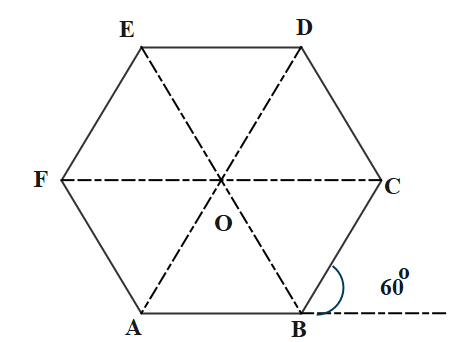
Let us assume that the motorist starts from point A.
He takes a third turn at point A.
So, the magnitude of the displacement is given as,
AD = AO + OD = 500 + 500 = 1000m
Now, the total distance covered by the motorist at the third turn is given as,
Total distance = AB + BC + CD = 500 + 500 + 500 = 1500m
Now, further the motorist takes a sixth at the point A, which is the starting point.
Magnitude of displacement of the motorist = 0
Total distance covered by the motorist is given as,
Total path covered = AB + BC + CD + DE + EF + FA = 6×500=3000m6 \times 500 = 3000m
At point C, the motorist takes the eight turn
Magnitude of displacement of the motorist = AC
By the triangle law, the magnitude of the displacement is given as 866.03m.
Total path covered by the motorist = 3000 + 500 + 500 = 4000m

Hence, the total path covered by the motorist is 4000m.

Note:
Triangle law of vector addition states that when two vectors are represented as two sides of the triangle with the order of magnitude and direction, then the third side of the triangle represents the magnitude and direction of the resultant vector.