Question

On a two lane road, car $A$ is travelling with a speed of $36{\text{ }}\dfrac{{km}}{{hr}}$. Two cars $B$ and $C$ approach car $A$ from opposite directions with speeds of ${\text{54 }}\dfrac{{km}}{{hr}}$ each. At a certain instant, when both car $B$ and $C$ are at a distance of $1{\text{ }}km$ from $A, B$ decides to overtake car $A$ before $C$ does. What minimum acceleration of B is required to avert an accident?

Answer 1

In this question we have two cases, in one we have to find the relative velocity of car C with respect to A and then find out the time needed for it to cross car A. In the other case, we have to find the distance B has to cover in order to overtake A. With the help of the time which is required by car C to cross car A, we will find the minimum acceleration that car B has to use in order to beat the time of car C to cover it and hence overtake A using motion’s equation.

Complete step by step answer:

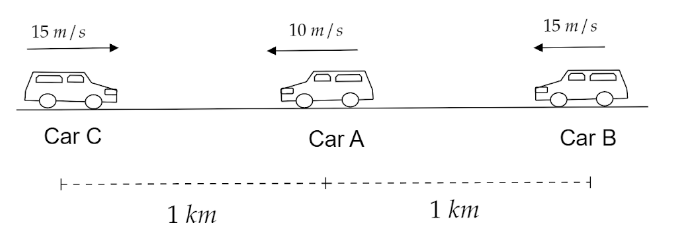
In the given question, the speed of car A$= 36{\text{ }}\dfrac{{km}}{{hr}} = 36 \times \dfrac{5}{{18}} = 10{\text{ }}\dfrac{m}{s}$.
The speed of car B$=$ speed of car C$= {\text{54 }}\dfrac{{km}}{{hr}} = 54 \times \dfrac{5}{{18}} = 15{\text{ }}\,\dfrac{m}{s}$.
As, the car C is in the opposite direction to the movement of car A, then relative velocity of car C with respect to A$= 15 + 10 = 25{\text{ }}\dfrac{m}{s}$.

The distance between A and C is given as $1{\text{ }}km = 1000{\text{ }}m$.
So, the time required by car C to cover the distance upto car A$= \dfrac{{1000}}{{25}} = 40{\text{ }}s$. Now, as the car B has to overtake car A before car C crosses car A then, it must do it exactly or just before $40{\text{ }}s$. In $40{\text{ }}s$, car A covers a distance$= 10 \times 40 = 400{\text{ }}m$In order to overtake car A, car B has to cover a total of $\left( {1000 + 400 = 1400{\text{ }}m} \right)$ and within the time $40{\text{ }}s$ or else car C will cross car A.

Let the acceleration required for this purpose be $a$.Using motion equation,
$s = ut + \dfrac{1}{2}a{t^2}$
where $s =$ distance$= 1400{\text{ }}m$, $u =$ velocity of car B$= 15{\text{ }}\dfrac{m}{s}$, $t =$ time$= 40{\text{ }}s$ and $a =$ acceleration.
Substituting the values we get,
$1400 = 15 \times 40 + \dfrac{1}{2} \times a \times {\left( {40} \right)^2} \\\ \Rightarrow 800 = 800a$
Dividing both sides by $800$ we get,
$a = 1$
So, the acceleration that car B has to gather in order to overtake car A before car C crosses it without any accident should be just greater than $1{\text{ }}\dfrac{m}{{{s^2}}}$.

Note: It must be noted that if car B has an acceleration of exactly $1{\text{ }}\dfrac{m}{{{s^2}}}$ then it will collide with car C as it will also cover the same distance within that same time. So, in order to avert a collision it must have an acceleration $> 1{\text{ }}\dfrac{m}{{{s^2}}}$. We have to consider relative velocity of car C , as the car A and C approaches towards each other and hence the distance between them decreases due to both of their movements, which is not true for car A and car B, so we have not considered relative velocity between car A and B.