Question

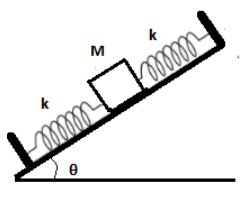
On a smooth inclined plane, a body of mass $M$ is attached between two springs. The other ends of the springs are fixed to firm supports. If each spring has force constant, $k$ , the period of oscillation of the body (Assuming the springs are massless) is:

$A.2\pi \sqrt{\dfrac{M}{2k}}$
$B.2\pi \sqrt{\dfrac{2M}{k}}$
$C.2\pi \sqrt{\dfrac{M\sin \theta }{2k}}$
$D.2\pi \sqrt{\dfrac{2Mg}{k}}$

Answer 1

The given problem is a combination of springs. Springs are connected by two ways. One is in series and the other is in parallel. The springs are connected in series in this case. We will also use the relation of angular frequency in terms of spring constant and mass.
Formula used: We are using following formulae to solve the problem:
$\dfrac{1}{{{k}_{eq}}}=\dfrac{1}{{{k}_{1}}}+\dfrac{1}{{{k}_{2}}}$ , $\omega =\sqrt{\dfrac{{{k}_{eq}}}{M}}$ and $T=\dfrac{2\pi }{\omega }$

Complete step by step solution:
We define spring as the device which stores potential energy by straining the bonds between the atoms of an elastic material.
We have the following figure with us:-

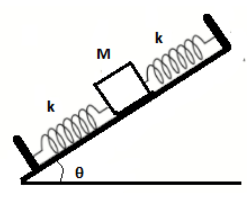
From the figure above we can clearly see that the springs are connected in series and they have the same spring constant $k$ , mass of the body is $M$ and $\theta$ is the angle with the horizontal. Therefore, their equivalent spring constant $({{k}_{eq}})$ will be given as follows:-
$\dfrac{1}{{{k}_{eq}}}=\dfrac{1}{{{k}_{1}}}+\dfrac{1}{{{k}_{2}}}$ ………………. $(i)$
Putting the values of spring constants in $(i)$ ,we get
$\dfrac{1}{{{k}_{eq}}}=\dfrac{1}{k}+\dfrac{1}{k}$
$\Rightarrow \dfrac{1}{{{k}_{eq}}}=\dfrac{2}{k}$
Therefore, ${{k}_{eq}}=\dfrac{k}{2}$ ………………… $(ii)$
Now, we will find the angular velocity $(\omega )$ for the oscillation by the use of following formula:-
$\omega =\sqrt{\dfrac{{{k}_{eq}}}{M}}$ ………………… $(iii)$
Now using the value of ${{k}_{eq}}$ from equation $(ii)$ and putting it in equation $(iii)$ , we get
$\omega =\sqrt{\dfrac{k}{2M}}$ ………………… $(iv)$
We have got the angular velocity of the oscillation now we will find the time period using the following equation:-
$T=\dfrac{2\pi }{\omega }$ …………. $(v)$
Putting the value of $\omega$ from equation $(iv)$ and putting it in equation $(v)$ we get
$T=\dfrac{2\pi }{\sqrt{\dfrac{k}{2M}}}$
$\Rightarrow T=2\pi \sqrt{\dfrac{2M}{k}}$

Therefore, option $(B)$ is correct.

Note:
Combination of springs is different from combination of resistances. The effective spring constant or force constant is simply the sum of individual spring constants in parallel combination. While in series combination, the reciprocal of effective spring constant is equal to the sum of reciprocal of individual spring constant. We should also give our attention towards correct use of formulae.