Question
Question: On a pulley of mass \( M \) hangs a rope with two masses \( {m_1} \) and \( {m_2} \) \( ({m_1} > {m_...
On a pulley of mass M hangs a rope with two masses m1 and m2 (m1>m2) tied at the ends as shown in the figure. The pulley rotates without any friction whereas the friction between the rope and the pulley is large enough to prevent any slipping. Which of the following plots best represents the difference between the tensions in the rope on the two sides of the pulley as a function of the mass of the pulley?
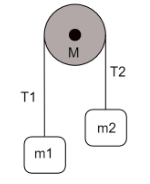
(A) 
(B) 
(C) 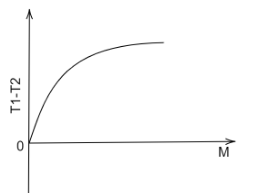
(D) 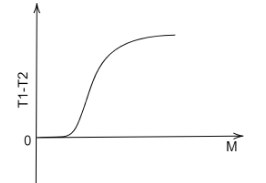
Solution
In order to find the difference, we first draw the free body diagrams of both masses, and balance the forces. We then add both of these equations, this is the first equation. The torque on the pulley is then equated with the tension in the rope, which gives rise to a second equation. Both of these equations are then combined to define the relation of T1−T2 with mass of the pulley M .
Complete step by step solution
It is given in the question that the pulley rotates without friction and the rope connecting the masses m1 and m2 does not slip.
It is also mentioned that m1>m2 . This means that the rope will move towards m1 and it will go down while m2 will accelerate upwards.
As they both are connected via rope, the acceleration of both blocks would be the same, but in opposite directions.
Therefore drawing the free body diagrams of both masses assuming these conditions,
For block m1 ,
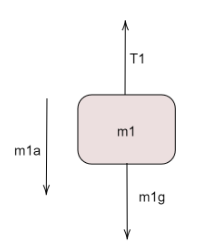
Balancing the vertical forces and acceleration,
m1a=m1g−T1 …(a)
For block m2 ,
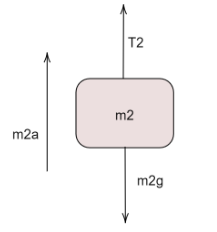
Balancing the vertical forces and acceleration,
m2a=T2−m2g …(b)
Adding equations (a) and (b), we obtain-
m1a+m2a=m1g−T1+T2−m2g
On rearranging this,
(m1+m2)a=(m1−m2)g−(T1−T2) … (1)
Now, on drawing the free body diagram of the pulley,

We see an angular acceleration of the pulley, which is caused by the turning of the rope around it, therefore the linear component of this acceleration must be equal to the torque produced by the rope.
τ=(T1−T2)r ...(c)
(The difference in the tensile forces is used as the torque to produce rotation in the pulley.)
Also,
τ=Iα
where α is the angular acceleration of the pulley while I is the moment of inertia of the pulley.
For a circular disk, the Moment of inertia about its central axis of rotation is given by,
I=2mr2
Keeping the mass of the pulley equal to M and its radius equal to r ,
The torque is,
τ=2Mr2α …(d)
On equating (c) and (d) we get,
τ=(T1−T2)r=2Mr2α
⇒T1−T2=2Mrα
Writing in terms of linear acceleration using the relation,
a=rα
we have,
T1−T2=2Ma
a=M2(T1−T2) … (2)
Substituting the value of a in equation (1) , we get-
(m1+m2)(M2(T1−T2))=(m1−m2)g−(T1−T2)
Dividing both sides with T1−T2 ,
(m1+m2)(M2)=T1−T2(m1−m2)g−1
⇒M2(m1+m2)+1=T1−T2(m1−m2)g
Upon cross multiplying we get,
T1−T2=(M2(m1+m2)+1)(m1−m2)g
⇒T1−T2=2(m1+m2)+MM(m1−m2)g
M is present in both, the numerator and the denominator of the relation.
As the value of M is increased, the difference in the values of T1 and T2 diminishes.
Therefore, the graph which best represents this relation is option (C), hence it is the answer.
Note
For a fixed value of m1 and m2 , since m1>m2 the numerator always remains a positive quantity. With the increase in the value of M , the overall value of the term increases but the rate of this increment slows down.
