Question
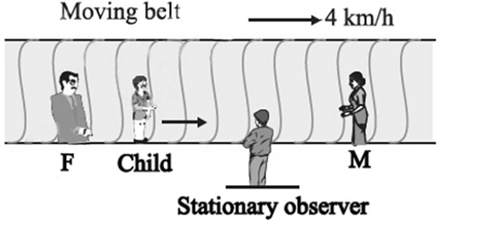
Question: : On a long horizontally moving belt (Fig), a child runs to and fro with speed 9km/h ( with respect ...
: On a long horizontally moving belt (Fig), a child runs to and fro with speed 9km/h ( with respect to the belt) between his father and mother located 50m apart on the moving belt. The belt moves with a speed of 4km/h. For an observer on a stationary platform outside, what is the
a) Speed of the child running in the direction of the belt.
b) Speed of child running opposite in the direction of motion of the belt.
c) Time is taken by the child (a) and (b).
Solution
Hint:- The relative velocity of an object A with respect to another object B is the time rate at which the object A changes its position with respect to the object B. To solve this problem, we used the relative velocity formula to calculate the speed of the child in the direction and opposite to the direction of motion of the belt.
Formula used: For the same direction VBA=(VB−VA)
Also for opposite direction VBA=(−VB−VA)
Complete step-by-step solution :i) According to given data,
Speed of the belt =4kmh−1
Speed of the child with respect to belt (Vcb) =9kmh−1
⇒Vcb=Vc−Vb
⇒9kmh−1=Vc−4kmh−1
⇒Vc=(9+4)kmh−1=13kmh−1
Therefore the speed of child running in the direction of motion of the belt =13kmh−1
ii) Now, the child runs in the opposite direction.
The speed of the belt =4kmh−1
Speed of the child with respect to belt (Vcb) =−9kmh−1
(Here negative sign indicates that child run in opposite direction)
⇒Vcb=Vc−Vb
⇒−9kmh−1=Vc−4kmh−1
⇒Vc=(−9+4)kmh−1=−5kmh−1
Therefore the speed of child running in the opposite direction of motion of the belt =−5kmh−1
iii) The speed of the child observed by the stationary observers (i.e. mother and father) both presents on the same belt. When a child runs there is only change in direction; it becomes positive in the same direction and negative in the opposite direction.
So the time taken by the child in both cases, Time=SpeedDistance ………(1)
Given distance =50m
Also the speed of the child given in forward and backward direction =9kmh−1=9×185=2.5m/s
Now, substitute the value in equation (1) we get,
Time=2.5m/s50m=2550×10=20sec
Therefore the time taken by the child in case of (a) and (b) =20sec
Note:- In the above question two different frames are involved i.e. an inertial frame and a stationary frame. It depends on the observer on which he is standing and the motion of the object seen by the observer on each of these frames will be different.
