Question

On a graph paper, plot the point $A\left( {2,3} \right)$, $B\left( {6, - 1} \right)$ and ${\rm{C}}\left( {0,5} \right)$, if those points collinear then draw the line which includes them. Write the co-ordinates of the points which the line intersects the $x$-axis and $y$-axis. The answer is $X$ axis$\left( {n,0} \right)$ and $Y$ axis $\left( {0,m} \right)$ then the value of $\left( {m + n} \right)$ is

Answer 1

Here we have to find the relation between $m$ and $n$. As all the three points A, B and C are collinear. We will first draw a line joining these three points and mark the points where it cuts the $x$-axis and $y$-axis and then we will find the slope of the line using any two points of it. We will use this value of slope to find the coordinates of $x$-axis and $y$-axis by applying the slope formula to get the value of$\left( {m + n} \right)$ then.

Complete step-by-step answer:
It is given that the points $A\left( {2,3} \right)$, $B\left( {6, - 1} \right)$ and ${\rm{C}}\left( {0,5} \right)$ are collinear.
We will plot all the three points and then will draw the line joining these three points. We will mark the point where it cuts the $x$-axis and $y$-axis as $X\left( {n,0} \right)$ and $Y\left( {0,m} \right)$.

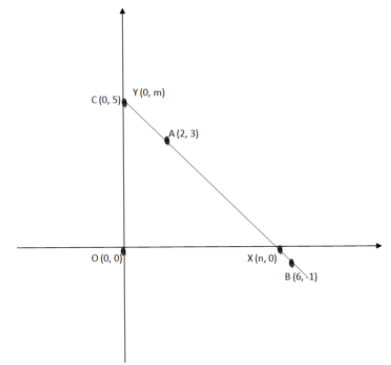
From the figure, we can see that the point C and point Y are the same, so the value of their coordinates will be the same.
Therefore,
$C\left( {0,5} \right) = Y\left( {0,m} \right)$
Hence, the value of $m$ is 5.
Now, we will find the slope of the line using the points $A\left( {2,3} \right)$ and $B\left( {6, - 1} \right)$.
Slope of line $= \dfrac{{ - 1 - 3}}{{6 - 2}}$
Simplifying the terms, we get
Slope of line $= \dfrac{{ - 4}}{4} = - 1$
We will use the slope formula using points $X\left( {n,0} \right)$ and $A\left( {2,3} \right)$
Slope of line $= \dfrac{{3 - 0}}{{2 - n}} = \dfrac{3}{{2 - n}}$
Substituting the value of the slope, we get
$\Rightarrow$ $- 1 = \dfrac{3}{{2 - n}}$
On cross multiplication, we get
$\Rightarrow$ (n - 2) = 3
$\Rightarrow$ n = 5
Thus, the value of $n$ is 5.
Now we will find the value of $\left( {m + n} \right)$.
Substituting the value of $m$ and $n$, we get.
$\Rightarrow$ (m + n)
= 5 + 5
= 10
This is the required answer.

Note: Here we have calculated the value of slope of the given line. A slope is also known as gradient and it is the ratio of the difference of $y$ coordinates to the difference of the $x$ coordinates.
Some important properties of slope are:-
(i)If the value of slope is greater than zero then the line goes up from left to right.
(ii)If the value of slope of the line is less than zero then the line goes down from right to left.
(iii)The value of slope for horizontal lines is zero.
(iv)The value of slope is not defined for vertical lines.