Question

On a frictionless horizontal surface, assumed to be the x-y plane., a small trolley A is moving along a straight line parallel to the y-axis with a constant velocity of $(\sqrt{3} -1 ) ms^{-1}$. At a particular instant, when the OA line makes an angle of $45^{\circ}$ with the axis, a ball is thrown along the surface from the origin O. Its velocity makes an angle $\phi$ with the x-axis and it hits the trolley.

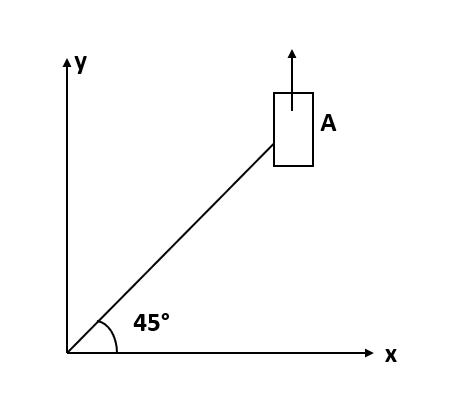
a. The motion of the ball is observed from the frame of the trolley. Calculate the angle $\theta$ made by the velocity vector of the ball with the x-axis in this frame.
b. Find the speed of the ball with respect to the surface, if $\phi = \dfrac{4 \theta}{3}$ .

Answer 1

First, we will find the direction of the ball with the surface, after getting all the directions, we will make a diagram to show all angles and velocities. After that, we will have the speed of the ball with respect to the surface. After putting all the values, we will find the speed of the ball.

Complete step by step answer:
a) Since the ball strikes the trolley, with respect to the relative to the trolley, the velocity of the ball should be pointed towards the trolley. Hence, in the trolley frame, the ball will seem to be travelling towards OA, or in the trolley frame, the ball's velocity will create an angle of $45^{\circ}$.

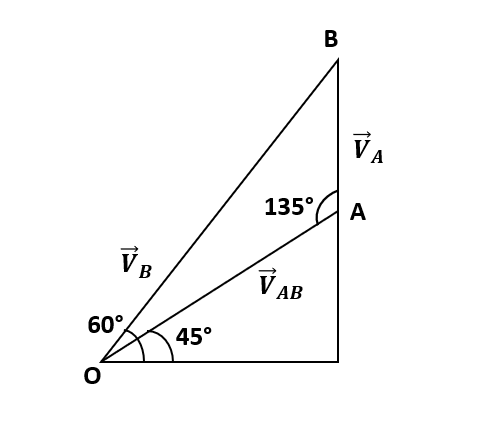
b) First, we find the angle that ball makes an angle with the surface.
$\phi = \dfrac{4 \theta}{3}$
$\theta = 45^{\circ}$
$\phi = \dfrac{4 \times 45}{3} = 60^{\circ}$
We will use sine rule,
$\dfrac{V_{B}}{sin 135^{\circ}} = \dfrac{V_{A}}{sin 15^{\circ}}$
$V_{A} = \sqrt{3} – 1 = 0.732 ms^{-1}$
$V_{B} = \dfrac{V_{A}}{sin 15^{\circ}} \times sin 135^{\circ}$
$\implies V_{B} = \dfrac{0.732}{0.2588} \times 0.707$
$\implies V_{B} = 2.00 ms^{-1}$

Note: The basic theory of relative speed is that when two bodies travel in an identical direction, the relative speed of one body concerning the other is the opposition between the two. Moreover, when the two bodies are traveling in the opposite direction, the relative speed of one body concerning the other is the total of the speeds of the two.