Solveeit Logo
Login

Question

Question: On a bright sunny day, a diver of height \(h\) stands at the bottom of a lake of depth \(H\). Lookin...

On a bright sunny day, a diver of height hh stands at the bottom of a lake of depth HH. Looking upward, he can see objects outside the lake in a circular region of radius RR. Beyond this circle he sees the images of objects lying on the floor of the lake. If refractive index of water is 43\dfrac{4}{3}, then the value of RR is:
A. 3(H−h)/73\left( {H - h} \right)/\sqrt 7
B. (H−h)/7/3\left( {H - h} \right)/\sqrt {7/3}
C. 3h73h\sqrt 7
D. 3(H−h)/5/33\left( {H - h} \right)/\sqrt {5/3}

Explanation

Solution

Here first we have to assume and draw the observations given in the question, and then we have to find the critical angle to and use snell’s law to get the radius RR

Complete step by step solution:
First let us see what refractive index is:
Refractive index is the ratio between the speed of light in vacuum and its speed in a given medium.
The refractive index does not have any dimension. It is a ratio representing the number of times slower a light wave would be in the given material than it is in a vacuum. The velocity of light in vacuum divided by the velocity of light in the medium is the refractive index.

Now let us observe the points given in the question.
Height of the diver =h = h

Height of the lake =H = H

Radius outside the lake =R = R

Refractive index of water =43 = \dfrac{4}{3}

It is given that a diver of height hh stands at the bottom of a lake of depth HH. Looking upward, he can see objects outside the lake in a circular region of radius RR. Beyond this circle he sees the images of objects lying on the floor of the lake.
We have to find the value of RR.


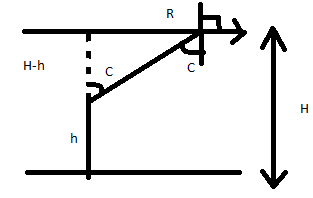
Let C be the critical angle of the refracted image formed with respect to the man.
Applying snell’s law on angle C we get-
μ1sin⁡C=μ2sin⁡90∘ ⇒43sin⁡C=1×1 ⇒43sin⁡C=1 ⇒sin⁡C=34 {\mu _1}\sin C = {\mu _2}\sin {90^ \circ } \\\ \Rightarrow \dfrac{4}{3}\sin C = 1 \times 1 \\\ \Rightarrow \dfrac{4}{3}\sin C = 1 \\\ \Rightarrow \sin C = \dfrac{3}{4} \\\
(refractive index of μ1=43{\mu _1} = \dfrac{4}{3} and μ2=1{\mu _2} = 1)
Therefore, tan⁡C=37\tan C = \dfrac{3}{{\sqrt 7 }}

From the figure we can see
Also,
tan⁡C=RH−h 37=RH−h R=3(H−h)7  \tan C = \dfrac{R}{{H - h}} \\\ \dfrac{3}{{\sqrt 7 }} = \dfrac{R}{{H - h}} \\\ R = \dfrac{{3\left( {H - h} \right)}}{{\sqrt 7 }} \\\

Hence, option A is correct.

Note: Here we have to observe and assume how light is refracted in the figure with respect to the man. Also we have to keep in mind what snell’s law is and how it affects the refractive index.