Question

On a body of mass ${{m}_{1}}$, certain force is applied which produces an acceleration of $6m{{s}^{-2}}$. The same force applied on mass ${{m}_{2}}$ gives it an acceleration of$4m{{s}^{-2}}$. If the two masses are fixed together and the same force is applied to the combination then find the acceleration it would produce.

& \text{A) }2.4\text{m}{{\text{s}}^{\text{-2}}} \\\ & \text{B) 3}\text{.4m}{{\text{s}}^{-2}} \\\ & \text{C) 4}\text{.4m}{{\text{s}}^{-2}} \\\ & \text{D) 2m}{{\text{s}}^{-2}} \\\ \end{aligned}$$

Answer 1

We need to understand the relation between the force acting on a body, its acceleration and the mass of the object to solve this problem. The derivation of Newton's second law of motion will give the solution to this problem right away.

Complete step by step solution:
According to Newton's second law of motion, the rate of change of momentum of an object will result in an acceleration of the object. We know that the rate of change of momentum is defined to be the external force acting on the object of a given mass. We have derived the formula connecting the force acting on the body, its mass and the acceleration from this law as –
$F=ma$

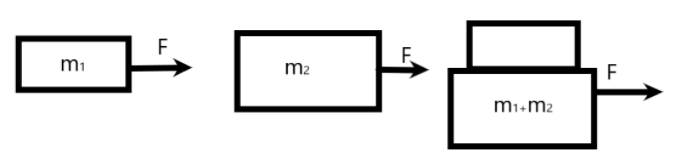
Now, we are given a situation in which a force F is acting on two objects. It is also given that the acceleration produced by the force on these two bodies are different. This gives us the hint that the two masses are unequal. We can use the formula given above to find the mass of the two bodies as –

& F=ma \\\ & \Rightarrow F={{m}_{1}}{{a}_{1}} \\\ & {{a}_{1}}=6m{{s}^{-2}} \\\ & \Rightarrow F=6{{m}_{1}} \\\ & \Rightarrow {{m}_{1}}=\dfrac{F}{6}\text{ -(1)} \\\ \end{aligned}$$ $$\begin{aligned} & \text{Also,} \\\ & F={{m}_{2}}a \\\ & \text{given,} \\\ & a=4m{{s}^{-2}} \\\ & \Rightarrow F=4{{m}_{2}} \\\ & \Rightarrow {{m}_{2}}=\dfrac{F}{4}\text{ --(2)} \\\ \end{aligned}$$ Now, we are given that the two masses are fixed together and the same force is applied, we can find the acceleration due to the system using the values masses from (1) and (2) as – $$\begin{aligned} & F=ma \\\ & \Rightarrow F=({{m}_{1}}+{{m}_{2}})a \\\ & \Rightarrow F=(\dfrac{F}{6}+\dfrac{F}{4})a \\\ & \Rightarrow F=\dfrac{10F}{24}a \\\ & \therefore a=2.4m{{s}^{-2}} \\\ \end{aligned}$$ The acceleration of the system of masses is 2.4$$m{{s}^{-2}}$$. **The correct answer is option A.** **Note:** The force acting on a system of masses can be found by vectorially adding the force acting on each of the bodies in the system. The acceleration produced is the direct effect of the force applied to the system and the mass is the quantity that determines the force required.