Solveeit Logo
Login

Question

Question: of $\lim_{x\to 1} \frac{(x^2-1)\sin^2(\pi x)}{x^4-2x^3+2x-1}$...

of lim⁡x→1(x2−1)sin⁡2(πx)x4−2x3+2x−1\lim_{x\to 1} \frac{(x^2-1)\sin^2(\pi x)}{x^4-2x^3+2x-1}

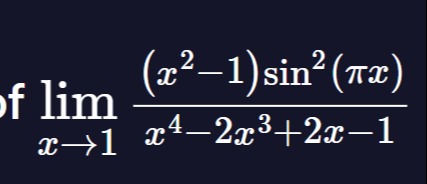
Answer

π2\pi^2

Explanation

Solution

  1. The limit is of the indeterminate form 00\frac{0}{0}.
  2. Factorize the denominator: x4−2x3+2x−1=(x2−1)(x−1)2x^4-2x^3+2x-1 = (x^2-1)(x-1)^2.
  3. Simplify the limit expression by canceling (x2−1)(x^2-1): lim⁡x→1sin⁡2(πx)(x−1)2\lim_{x\to 1} \frac{\sin^2(\pi x)}{(x-1)^2}.
  4. Substitute y=x−1y=x-1. The limit becomes lim⁡y→0sin⁡2(π(y+1))y2\lim_{y\to 0} \frac{\sin^2(\pi(y+1))}{y^2}.
  5. Using sin⁡(π+θ)=−sin⁡(θ)\sin(\pi+\theta)=-\sin(\theta), this simplifies to lim⁡y→0sin⁡2(πy)y2\lim_{y\to 0} \frac{\sin^2(\pi y)}{y^2}.
  6. Rewrite as lim⁡y→0(sin⁡(πy)y)2\lim_{y\to 0} \left(\frac{\sin(\pi y)}{y}\right)^2.
  7. Apply the standard limit lim⁡z→0sin⁡(az)z=a\lim_{z\to 0} \frac{\sin(az)}{z} = a.
  8. The result is (π)2=π2(\pi)^2 = \pi^2.