Question

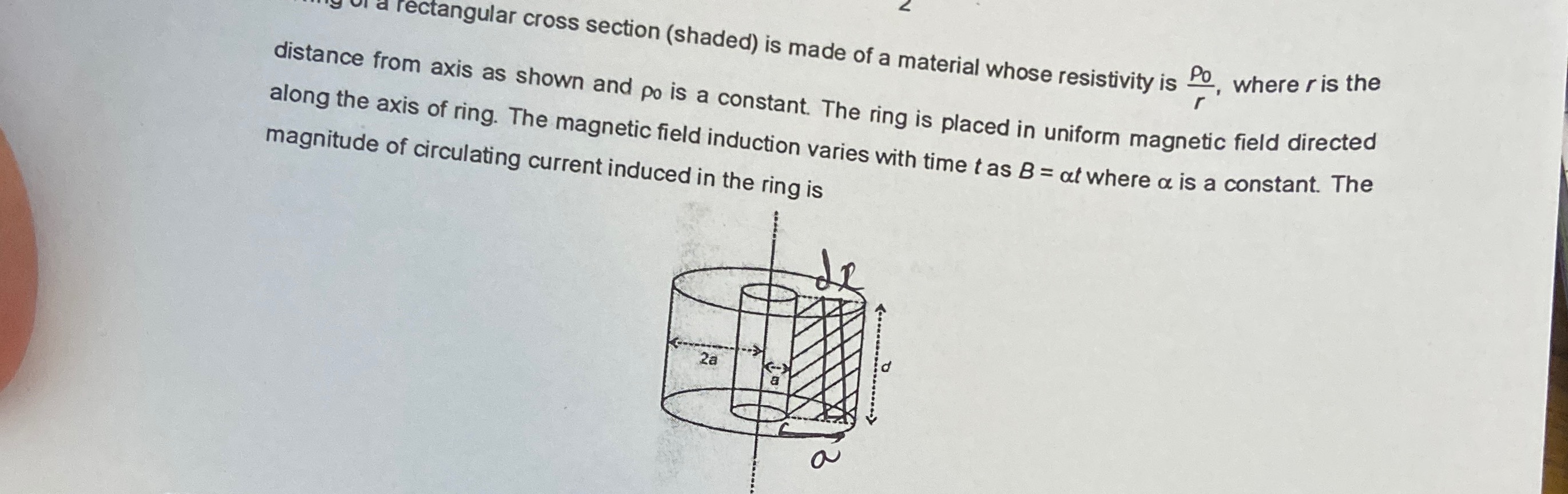
of a rectangular cross section (shaded) is made of a material whose resistivity is $\frac{\rho_0}{r}$, where r is the distance from axis as shown and $\rho_0$ is a constant. The ring is placed in uniform magnetic field directed along the axis of ring. The magnetic field induction varies with time t as $B = \alpha t$ where $\alpha$ is a constant. The magnitude of circulating current induced in the ring is

Answer 1

$\frac{7 \alpha d a^3}{6\rho_0}$

Answer 2

The problem asks for the magnitude of the circulating current induced in a ring with a rectangular cross-section. The resistivity of the material varies with the distance from the axis. A uniform magnetic field, varying with time, is directed along the axis of the ring.

Here's a step-by-step derivation:

1. Induced Electromotive Force (EMF) and Electric Field: The magnetic field is given as $B = \alpha t$, directed along the axis. Consider a circular loop of radius $r$ within the material of the ring. The area enclosed by this loop is $A = \pi r^2$. The magnetic flux $\Phi_B$ through this loop is: $\Phi_B = B \cdot A = (\alpha t)(\pi r^2)$ According to Faraday's Law of Electromagnetic Induction, the magnitude of the induced EMF ($\mathcal{E}$) around this loop is: $\mathcal{E} = \left| -\frac{d\Phi_B}{dt} \right| = \left| -\frac{d}{dt}(\alpha t \pi r^2) \right| = \alpha \pi r^2$ This induced EMF is also related to the induced electric field $E(r)$ by the line integral around the loop: $\mathcal{E} = \oint \vec{E} \cdot d\vec{l}$ Due to the cylindrical symmetry, the induced electric field $E(r)$ will be tangential and uniform along the circumference for a given radius $r$. $E(r) \cdot (2\pi r) = \alpha \pi r^2$ Solving for $E(r)$: $E(r) = \frac{\alpha \pi r^2}{2\pi r} = \frac{\alpha r}{2}$

2. Resistivity and Conductivity: The resistivity of the material is given as $\rho(r) = \frac{\rho_0}{r}$. The conductivity $\sigma(r)$ is the reciprocal of resistivity: $\sigma(r) = \frac{1}{\rho(r)} = \frac{1}{\frac{\rho_0}{r}} = \frac{r}{\rho_0}$

3. Current Density: The current density $J(r)$ at a radius $r$ is given by Ohm's Law in differential form: $J(r) = \sigma(r) E(r)$ Substitute the expressions for $\sigma(r)$ and $E(r)$: $J(r) = \left(\frac{r}{\rho_0}\right) \left(\frac{\alpha r}{2}\right) = \frac{\alpha r^2}{2\rho_0}$

4. Total Circulating Current: The current flows circumferentially around the axis. To find the total current, we consider an infinitesimal cylindrical shell of radius $r$ and radial thickness $dr$. The height of the ring is $d$. The cross-sectional area $dA$ through which the current $dI$ flows (perpendicular to the current density $J(r)$) is: $dA = d \cdot dr$ The infinitesimal current $dI$ through this shell is: $dI = J(r) \cdot dA = \left(\frac{\alpha r^2}{2\rho_0}\right) (d \cdot dr)$ To find the total circulating current $I$ in the ring, we integrate $dI$ from the inner radius $a$ to the outer radius $2a$: $I = \int_{a}^{2a} dI = \int_{a}^{2a} \frac{\alpha d r^2}{2\rho_0} dr$ $I = \frac{\alpha d}{2\rho_0} \int_{a}^{2a} r^2 dr$ $I = \frac{\alpha d}{2\rho_0} \left[ \frac{r^3}{3} \right]_{a}^{2a}$ $I = \frac{\alpha d}{2\rho_0} \left( \frac{(2a)^3}{3} - \frac{a^3}{3} \right)$ $I = \frac{\alpha d}{2\rho_0} \left( \frac{8a^3}{3} - \frac{a^3}{3} \right)$ $I = \frac{\alpha d}{2\rho_0} \left( \frac{7a^3}{3} \right)$ $I = \frac{7 \alpha d a^3}{6\rho_0}$

The magnitude of the circulating current induced in the ring is $\frac{7 \alpha d a^3}{6\rho_0}$.