Question

Obtain the relation between linear velocity and angular velocity.

Answer 1

At first we need to find the formula for angular velocity. We need to draw figures that satisfy the question and help us in solving the question. After that we need to find the angular velocity for one complete rotation. Then we need to find the formula for linear velocity. Then need to replace some part of the formula with other relations that we will get while solving to get the required result.

Formulas used:
ds = v dt
$\omega =\dfrac{d\theta }{dt}$
$\omega =\dfrac{\theta }{t}=\dfrac{2\pi }{T}$
$d\theta =\dfrac{vdt}{r}$
$v=\omega r$

Complete step by step answer:
At first we need to know the definition of angular velocity,
The rate of change of angular displacement is known as the angular velocity of the particle.

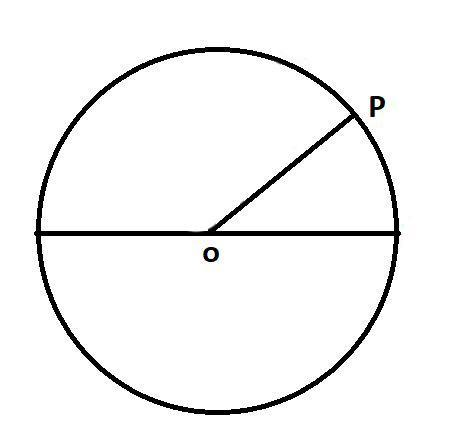
In the above diagram, P is the particle which is moving in a fixed circular path, now let us consider $d\theta$ , as the angular displacement made by the particle in a fixed time, let us consider that time as $dt$.
Then we know that, we can represent angular velocity the particle as,
$\omega =\dfrac{d\theta }{dt}$.
The dimensional formula for angular velocity of the particle is ${{T}^{-1}}$ and its SI unit is $rad\text{ }{{s}^{-1}}$.
Now if we consider that the particle has gone through a complete revolution, then the angle covered by the radius vector is $2\pi \text{ }radians$ or ${{360}^{\circ }}$. Now if time taken for one complete revolution is ‘T’ seconds, then the angular velocity of the particle is
$\omega =\dfrac{\theta }{t}=\dfrac{2\pi }{T}$
Now, if we say that the particle is making n revolutions per seconds, then the angular velocity will be,
$\omega =2\pi \left( \dfrac{1}{T} \right)=2\pi n$

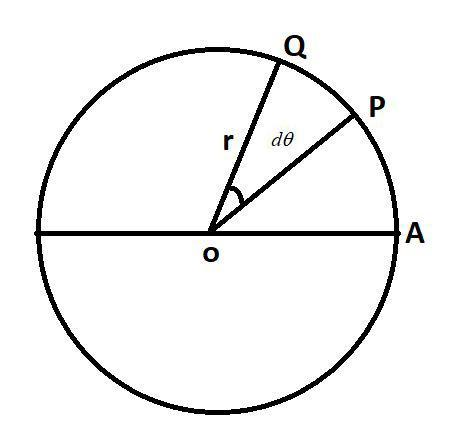
Now, in the above diagram, we see the particle is moving from point P to point Q, let us consider the distance as PQ=ds, and the angle covered by the particle is $d\theta$, so we can represent angular displacement $d\theta =\dfrac{ds}{r}$, but we know that ds = v dt.
$\dfrac{d\theta }{dt}=\dfrac{v}{r}$,
So, angular velocity is $\omega =\dfrac{v}{r}$ or $v=\omega r$.
Now, in vector notation, $\vec{v}=\vec{\omega }\times \vec{r}$
We already know that ds = v dt.
Therefore, $d\theta =\dfrac{vdt}{r}$ , or we can say
$\dfrac{d\theta }{dt}=\dfrac{v}{r}$ ,
So we can further solve it as,
Angular velocity, $\omega =\dfrac{v}{r}$or $v=\omega r$
In vector notation, $\vec{v}=\vec{\omega }\times \vec{r}$.
Therefore we can see that this is the relation between linear velocity and angular velocity.

Note:
We can say that for a given angular velocity, the linear velocity of the particle is directly proportional to the distance of the particle with respect to the centre of the circular path, that is we can write that for a body in a uniform circular motion, the angular velocity is different for different points of the body.