Question

Obtain the expression for the deflecting torque acting on the current-carrying rectangular coil of a galvanometer in a uniform magnetic field. Why is a radial magnetic field employed in the moving coil galvanometer?

Answer 1

A moving coil galvanometer is a device used to detect or measure very small currents. It works on the principle that when current flows through a rectangular coil kept in a magnetic field, it is deflected. The angle of deflection is proportional to the current through the coil.

Complete step by step solution:
Let us consider a rectangular coil $ABCD\;$. A current $I$ is flowing through the coil. Let $N$ be the number of turns of the coil and a uniform magnetic $B$ is along the x-axis.

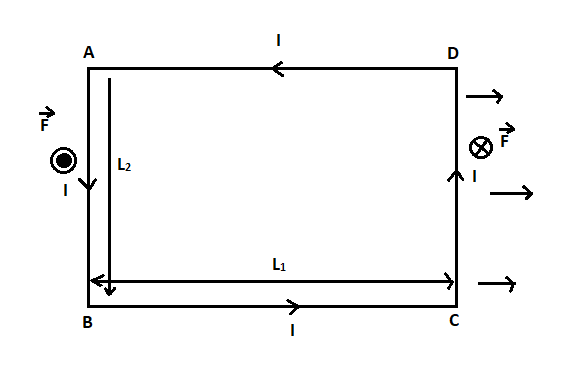
There will be a force acting on $AB\;$ and $CD\;$ since they are perpendicular to the direction of the magnetic field. Since $AD\;$ and $BC\;$ is along the direction of the magnetic field the force on these sides will be zero. Since the magnetic field $B\;$ is uniform and the same current is flowing through the coil, the force on $AB\;$ and $CD\;$ will be equal in magnitude and opposite in direction.

Let $\theta$ be the angle turned by the coil.
The force can be written as,
$F = \left( {I{l_2}B} \right)N\hat k$
Where $I$ stands for the current, ${l_2}$ is the breadth of the rectangle, $B$ is the magnetic field, $N$ is the number of turns, and $\hat k$ shows that the direction of force is in the $Z$ direction.
The torque can be written as,
$\tau = \dfrac{{F \times {l_1}}}{2}\sin \theta + \dfrac{{F \times {l_1}}}{2}\sin \theta$
This can be written as,
$\tau = \left( {\dfrac{{F{l_1}\sin \theta }}{2}} \right) \times 2$
Substituting the value of force in this equation, we get
$\tau = \left( {\dfrac{{BI{l_1}{l_2}\sin \theta }}{2}} \right) \times 2N$
This equation can be rearranged as,
$\tau = NIB{l_1}{l_2}\sin \theta$
Let $A$ be the area of the rectangular coil,
$A$ can be written as
$A = {l_1}{l_2}$
Now we can write the above equation as,
$\tau = NIAB\sin \theta$
Let $NIA = \vec M$
Where $\vec M$ is the magnetic moment of the coil.
Substituting, we get
$\tau = \vec M\vec B\sin \theta$
This is the cross product of $\vec M$ and $\vec B$.
$\tau = \vec M \times \vec B$.

Note:
The current-carrying coil rotates due to the torque. The suspension wire is twisted. A restoring couple is developed in the suspension wire. A steady deflection $\theta$ is produced when the restoring couple balances the torque produced. At equilibrium, the torque is proportional to the restoring couple.