Question

Obtain the expression for deflecting torque acting on the current carrying rectangular coil of a galvanometer in a uniform magnetic field. Why is a radial magnetic field employed in the moving coil galvanometer?

Answer 1

We know that the twisting force that tends to cause rotation is called torque. We also know that a device that detects and measures currents of small magnitudes is called a galvanometer. We will consider the basic mechanism of torque to find the solution.
Formula Used:
We are going to use the following formula to solve the given problem:-
$\tau =\dfrac{F\times l}{2}\times \sin \theta +\dfrac{F\times b}{2}\times \sin \theta$.

Complete answer:
We have the following figure with us:

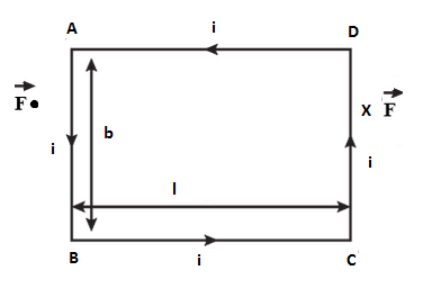
We consider a rectangular coil ABCD carrying the current $i$ and having $N$ number of turns. Then a uniform magnetic field $B$ exists in the coil in the x-direction.
Now, let the side BC and AD are along the magnetic field $B$. The force on BC and AD will be equal to zero and force will only act on AB and CD. Magnetic field $B$ is the same everywhere in the plane and the same current $(i)$ is also flowing throughout. Therefore, forces on AB and CD are equal and given as $(F)$ . If the coil is turned by an angle $\theta$ . Then, torque $(\tau )$ will be given as follows:-
$\tau =\dfrac{F\times l}{2}\times \sin \theta +\dfrac{F\times b}{2}\times \sin \theta$ …………. $(i)$
As force are equal and $l=b$, putting the values in $(i)$we get,
$\tau =\dfrac{2Fl\sin \theta }{2}$ .
But, $F=Bib$ , therefore, we get
$\Rightarrow \tau =\dfrac{2Bilb\sin \theta }{2}$
For $N$ turns it will be equal to
$\tau =NiBlb\sin \theta$ ………………… $(ii)$
But, area is the product of length and breadth.
$A=lb$ ……………… $(iii)$
Putting $(iii)$ in $(ii)$ we have
$\tau =NiAB\sin \theta$ ……………… $(iv)$
But magnetic moment, $M$ is given as follows:-
$M=NiA$ ……………… $(ii)$
Putting $(ii)$ in $(iv)$ we have,
$\tau =MB\sin \theta$
In vector form we can write it as follows:-
$\overrightarrow{\tau }=\overrightarrow{M}\times \overrightarrow{B}$
This is the required expression for torque.
We also know that the radial magnetic field is employed in a moving coil galvanometer to provide constant torque throughout which makes the deflection proportional to the current and one can measure galvanometer scale properly.

Note:
We should focus on the fact that the cross product of two vectors is a vector quantity. Therefore, the torque is a vector quantity which is the product of magnetic moment and magnetic field. Torque is maximum when magnetic moment and magnetic field are perpendicular to each other and torque is minimum when magnetic moment is in the direction of magnetic field.